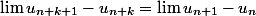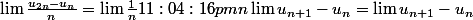Suite et limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 16 Sep 2014, 20:19
par smrh2002 » 16 Sep 2014, 20:19
Bonsoir
Je reste coincé sur le problème suivant
U(n) suite réelle lim(n->+inf) [U(2n)-U(n)]/n = l
Peut on affimer que lim (n->+inf) U(n+1)-U(n) = l ?
Si vous avez une piste pour commencer ...
Merci pour votre aide

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 16 Sep 2014, 20:27
par Sa Majesté » 16 Sep 2014, 20:27
Salut
En général dans ce genre d'exo, soit on pense que c'est vrai et on se lance dans la démo, soit on pense que c'est faux et on trouve un contre-exemple.
On peut se faire une idée en prenant des exemples de suites (Un).
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 16 Sep 2014, 20:55
par smrh2002 » 16 Sep 2014, 20:55
Merci. Je vais essayer de trouver un exemple de suite ..
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 18 Sep 2014, 18:54
par smrh2002 » 18 Sep 2014, 18:54
Bonsoir
J'ai testé sur deux suites et ça marche donc maintenant il faut démontrer que c'est vrai.
Par quel bout puis je attaquer ? Encadrement ? Récurrence ?
Merci
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 18 Sep 2014, 19:47
par keofran » 18 Sep 2014, 19:47

peut s'interpréter comme la distance moyenne entre 2 termes consécutifs pour n termes consécutifs quelconques, autrement dit :
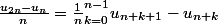
Que peut-on dire pour tout k de

?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 18 Sep 2014, 19:53
par Sa Majesté » 18 Sep 2014, 19:53
smrh2002 a écrit:J'ai testé sur deux suites et ça marche donc maintenant il faut démontrer que c'est vrai.
Essaie
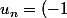^n)
-
keofran
- Membre Relatif
- Messages: 125
- Enregistré le: 12 Oct 2013, 00:39
- Localisation: Lyon
-
 par keofran » 18 Sep 2014, 20:22
par keofran » 18 Sep 2014, 20:22
Ah mince ! Je suis allé trop vite.
J'ai cru qu'on pouvait raisonner ainsi :
Pour tout k
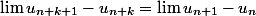
Donc
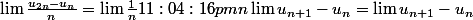
J'ai mélangé le fini et l'infini sans rigueur !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités