Exercice de reccurence

[terter60]

bonsoir

Pour demain j'ai un dm sur les récurrences a faire j'ai réussi les 3 premiers exercices mais ça fais plus d'une heures que je bloque sur le 4eme et il commence a se faire tard alors j'ai vraiment besoin d'aide...

Soit Sn=0+1+2+3+...+n
considérons la propriété Pn: Sn= 1/2(n+1/2)^2

a) démontrer que cette propriété est héréditaire
b) Pn est-elle vraie pour tout n de N

merci d'avance

[fatal_error]

salut,

ta propriété est fausse pour n=1
P1: S1= 1/2(1+1/2)^2=1/2(3/2)^2=1/2*9/4=9/8
or S1=0+1=1 ...

[mathelot]

bonjour,

ton égalité est fausse. la formule exacte est

(E_n)

la véracité de cette égalité (vraie ou fausse) dépend du rang n.

pour montrer l'hérédité, on la suppose vraie et on essaye d'en déduire laa
même au rang

on ajoute donc( n+1) de chaque côté de l'égalité pour passer de En à

[Tiruxa]

bonsoir

Pour demain j'ai un dm sur les récurrences a faire j'ai réussi les 3 premiers exercices mais ça fais plus d'une heures que je bloque sur le 4eme et il commence a se faire tard alors j'ai vraiment besoin d'aide...

Soit Sn=0+1+2+3+...+n
considérons la propriété Pn: Sn= 1/2(n+1/2)^2

a) démontrer que cette propriété est héréditaire
b) Pn est-elle vraie pour tout n de N

merci d'avance

le b) est évident car la propriété est fausse pour n=0, donc Pn est fausse.

Par contre elle est héréditaire

Supposons Pn vraie et démontrons que Sn+1=1/2(n+1+1/2)²

On a Sn+1=Sn+n+1=1/2(n+1/2)²+n+1

Il suffit de développer les deux expressions pour prouver l'égalité.

[terter60]

d'accord mais ensuite que dois je faire ? je suis désolée mais je ne comprend vraiment pas

[mathelot]

je te prie de m'excuser. je n'ai pas compris l'exercice


tu dois démontrer que l'égalité est toujours fausse mais héréditaire.

désolé

[mathelot]

d'accord mais ensuite que dois je faire ? je suis désolée mais je ne comprend vraiment pas

il s'agit de vérifier que la propriété est héréditaire
mais comme elle n'est jamais initialisée, en fait, elle est toujours fausse.

[terter60]

pas de problème mathelot

peux tu juste me m'etre sur la piste parce que j'ai du mal ?

[mathelot]

pour démontrer l'hérédité

on suppose que

en fait, cette hypothèse est toujours fausse, mais on suppose qu'elle est vraie,
car on a en vue de démontrer:



cette implication est vraie parfois avec p(n) fausse, l'hérédité et la véracité sont deux choses distinctes.

[terter60]

d'accord j'ai compris que la suite était fausse mais héréditaire mais je ne sais pas comment faire le déroulement pour le prouver

[mathelot]

d'accord j'ai compris que la suite était fausse mais héréditaire mais je ne sais pas comment faire le déroulement pour le prouver

bien joué !

tu démontre l'hérédité comme d'habitude.

on suppose au rang n

on ajoute des deux côtés de l'égalité et on trouve l''égalité

[terter60]

en ajoutant n+1 de chaque cotée de l'égalité je trouve (2n+3)^2/8 je crois que je me suis tromper

[Tiruxa]

en ajoutant n+1 de chaque cotée de l'égalité je trouve (2n+3)^2/8 je crois que je me suis tromper

Je continue mon message d'hier



Or




On a donc démontré la propriété à l'indice n+1, elle est donc héréditaire.

L'exercice a pour but de montrer que les deux étapes (initialisation, hérédité) de la démo sont importantes, même si l'hérédité est souvent la plus difficile à justifier elle ne suffit pas pour conclure.

[mathelot]

le b) est évident car la propriété est fausse pour n=0, donc Pn est fausse.

Par contre elle est héréditaire.

Notant .V.=vrai et .F.=faux, on a

et

par exemple, une inégalité comme



est héréditaire , dès le début ().

les propriétés fausses sont héréditaires (sans démonstration)

Sous l'hypothèse de récurrence, on démontre

(2)

Cette ligne démontre que la propriété est héréditaire pour

La propriété devient vraie pour n=6 (fausse avant)

[paquito]

Tu fais ton raisonnement normalement, mais en commençant par l'hérédité que tu prouves. Pour pouvoir appliquer le principe de récurrence tu dois alors vérifier que la propriété est vrai au rang n=0.

Ca te donne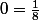, c'est faux, donc le principe de récurrence ne s'applique pas pour .

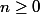Par contre ça ne prouve pas que Pn soit toujours fausse, mais que si P(n+1) est fausse alors Pn est fausse.

mathelot t'as donné un exemple où la propriété Pn était vrai à partir de n=6.

En ce qui concerne ton exemple, comme , on prouve que Pn est toujours fausse.

[Tiruxa]

les propriétés fausses sont héréditaires (sans démonstration)

En effet, on peut donc démontrer l'hérédité de (Pn) en justifiant que (Pn) est fausse pour tout n.

C'est assez évident car :

1/2(n+1/2)²=(2n+1)²/8

Or 2n+1 est impair pour tout entier n, donc n'est pas divisible par 8, donc (2n+1)²/8 n'est pas un entier il ne peut pas être égal à 1+2+3+...+n qui lui est entier.

(Pn) est faux pour tout n, donc (Pn) est héréditaire.