Triangle de Pascal
15 messages
- Page 1 sur 1
Triangle de Pascal
Bonjour, je sèche sur une question de maths, toute aide serait la bienvenue :
Lorsqu'on calcule le coefficient k parmi n à l'aide du triangle de Pascal, combien fait-on d'addition ?
Voici ce que j'ai trouvé à la main, p les colonnes et n les lignes :
0 0 0 0 0 0 0
0 1 0 0 0 0 0
0 2 2 0 0 0 0
0 3 4 3 0 0 0
0 4 6 6 4 0 0
0 5 8 9 8 5 0
0 6 10 12 12 10 6
Merci d'avance !
Lorsqu'on calcule le coefficient k parmi n à l'aide du triangle de Pascal, combien fait-on d'addition ?
Voici ce que j'ai trouvé à la main, p les colonnes et n les lignes :
0 0 0 0 0 0 0
0 1 0 0 0 0 0
0 2 2 0 0 0 0
0 3 4 3 0 0 0
0 4 6 6 4 0 0
0 5 8 9 8 5 0
0 6 10 12 12 10 6
Merci d'avance !
Bonjour.
Je ne vois pas où est le "triangle"
Que représentent les entiers écrits sue la même ligne? Est-ce que bien ce tu penses?
Trapnest a écrit:Bonjour, je sèche sur une question de maths, toute aide serait la bienvenue :
Lorsqu'on calcule le coefficient k parmi n à l'aide du triangle de Pascal, combien fait-on d'addition ?
Voici ce que j'ai trouvé à la main, p les colonnes et n les lignes :
0 0 0 0 0 0 0
0 1 0 0 0 0 0
0 2 2 0 0 0 0
0 3 4 3 0 0 0
0 4 6 6 4 0 0
0 5 8 9 8 5 0
0 6 10 12 12 10 6
Merci d'avance !
Je ne vois pas où est le "triangle"
Que représentent les entiers écrits sue la même ligne? Est-ce que bien ce tu penses?
deltab a écrit:Bonjour.
Je ne vois pas où est le "triangle"
Que représentent les entiers écrits sue la même ligne? Est-ce que bien ce tu penses?
J'ai écrit à la place de chaque coefficient le nombre d'addition qu'il faut effectuer pour l'obtenir.
On peut aussi le lire de cette manière :
0
0 1
0 2 2
0 3 4 3
0 4 6 6 4
0 5 8 9 8 5
0 6 10 12 12 10 6
Bonsoir plutôt Bonjour car je vais faire des modifications.
Je m'excuse, j'avais mal lu les énoncés.
Pour qu'on se retrouve plus facilement, il valait mieux numéroter les lignes et les colonnes et aligner les termes d'une colonne.
Les propriétés des coefficients binomiaux qu'on utilise habituellement pour construire le triangle de Pascal sont et
et  pour
pour 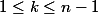 .
.  est calculé par cette formule, on n'utilise pas la propriété
est calculé par cette formule, on n'utilise pas la propriété  , idem pour
, idem pour 
Si on pose={n \choose k}) et
et ) =nombre d'additions à faire pour calculer
=nombre d'additions à faire pour calculer 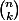 , on a alors
, on a alors = A(n,n)=0) et pour
et pour 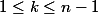 ,
,  =1+A(n-1,k-1) + A(n-1,k)) . Le terme
. Le terme  vient de l'addition
vient de l'addition  .
.
La construction du triangle du nombre d'additions) suit presque la méthode de construction du triangle de Pascal lui-même.
suit presque la méthode de construction du triangle de Pascal lui-même.
= A(n,n)=0)
 =1+A(n-1,k-1) + A(n-1,k))
PS: 1) Le terme A(n,n)(=0) ne figure pas dans le tableau que tu as donné.
2) Des premières lignes du triangle, il apparait que [/TEX]A(n,k) =A(n,n-k)[/TEX]. Cette propriété est-elle valable pour tout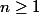 et
et  . (elle est trivialement vérifiée pour k=0 et k=n))
. (elle est trivialement vérifiée pour k=0 et k=n))
Je m'excuse, j'avais mal lu les énoncés.
Pour qu'on se retrouve plus facilement, il valait mieux numéroter les lignes et les colonnes et aligner les termes d'une colonne.
Les propriétés des coefficients binomiaux qu'on utilise habituellement pour construire le triangle de Pascal sont
Si on pose
La construction du triangle du nombre d'additions
PS: 1) Le terme A(n,n)(=0) ne figure pas dans le tableau que tu as donné.
2) Des premières lignes du triangle, il apparait que [/TEX]A(n,k) =A(n,n-k)[/TEX]. Cette propriété est-elle valable pour tout
Bonjour.
J'ai repris le triangle que tu as donné en numérotant les lignes (le numéro de la ligne correspond à la puissance) et en ajoutant A(n,n). L'alignement des colonnes est obtenu automatiquement en utilisant une matrice en LATEX.

Avec la construction que j'ai proposée, je trouve A(3,2)=2+2+1=5. Comment as-tu trouvé 4? Je ne parle pas des lignes d'ordre supérieur.
J'ai repris le triangle que tu as donné en numérotant les lignes (le numéro de la ligne correspond à la puissance) et en ajoutant A(n,n). L'alignement des colonnes est obtenu automatiquement en utilisant une matrice en LATEX.
Avec la construction que j'ai proposée, je trouve A(3,2)=2+2+1=5. Comment as-tu trouvé 4? Je ne parle pas des lignes d'ordre supérieur.
Bonjour, merci pour cette matrice.
J'ai choisi d'utiliser la convention suivante : on connait les 1 de la première colonne et de la diagonale, inutile donc de les calculer.
J'ai compris votre méthode qui se base sur la formule d'addition.
Il est vrai qu'elle est aussi applicable ici.
Voici la matrice modifiée avec la convention :

Cela laisse penser que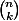 = (n-1)*k
= (n-1)*k
J'ai choisi d'utiliser la convention suivante : on connait les 1 de la première colonne et de la diagonale, inutile donc de les calculer.
J'ai compris votre méthode qui se base sur la formule d'addition.
Il est vrai qu'elle est aussi applicable ici.
Voici la matrice modifiée avec la convention :
Cela laisse penser que
Bonjour
Ce qui est totalement faux! Pour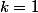 , on aurait eu
, on aurait eu 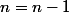 et pour
et pour 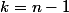 , on aurait eu
, on aurait eu 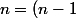^2)
Mais comment tu as trouvé que A(4,2)=6. Quelle est la méthode que tu as utilisée pour construire le triangle de Pascal, les valeurs des nombres A(n,k) en dépendent.
Si je te dis que pour le calcul de 115^2, j'utilise seulement deux additions , me croirais-tu? et que le calcul de 113 x 117 nécessite pour moi deux additions et une soustractions.
Si avec ma méthode, j'utilise aussi le fait que , alors A(n,1)=A(n,n-1)=0 et les valeurs A(n,k) vont changer.
, alors A(n,1)=A(n,n-1)=0 et les valeurs A(n,k) vont changer.

Trapnest a écrit:Bonjour, merci pour cette matrice.
J'ai choisi d'utiliser la convention suivante : on connait les 1 de la première colonne et de la diagonale, inutile donc de les calculer.
J'ai compris votre méthode qui se base sur la formule d'addition.
Il est vrai qu'elle est aussi applicable ici.
Voici la matrice modifiée avec la convention :
Cela laisse penser que= (n-1)*k
Ce qui est totalement faux! Pour
Mais comment tu as trouvé que A(4,2)=6. Quelle est la méthode que tu as utilisée pour construire le triangle de Pascal, les valeurs des nombres A(n,k) en dépendent.
Si je te dis que pour le calcul de 115^2, j'utilise seulement deux additions , me croirais-tu? et que le calcul de 113 x 117 nécessite pour moi deux additions et une soustractions.
Si avec ma méthode, j'utilise aussi le fait que
deltab a écrit:Bonjour
Ce qui est totalement faux! Pour, on aurait eu
et pour
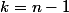
Mais comment tu as trouvé que A(4,2)=6. Quelle est la méthode que tu as utilisée pour construire le triangle de Pascal.
Si avec ma méthode, j'utilise aussi le fait que, alors A(n,1)=A(n,n-1)=0 et les valeurs A(n,k) vont changer.
Pour trouver ces coefficients, je ne rempli pas toutes les lignes, je cherche simplement à faire le moins d'addition possible pour partir de la base [1 1] de la première ligne et arriver au coefficient souhaité. Le chemin le plus court, donc.
Je n'utilise pas non plus
En effet la formule était stupide, je l'ai simplement testé sur un cas qui marchait et je n'ai pas pensé à vérifier les autres...
(n-k)*k ?
Bonjour
Peux-tu me donner le chemin le plus court pour obtenir A(4,2)=4? et la méthode que tu utilises pour construire le triangle de Pascal, il y en a bien une méthode. Tant que tu ne m'expliques pas ta méthode, je ne peux rien dire concernant les valeurs des A(n,k) que tu trouves.
Trapnest a écrit:Pour trouver ces coefficients, je ne rempli pas toutes les lignes, je cherche simplement à faire le moins d'addition possible pour partir de la base [1 1] de la première ligne et arriver au coefficient souhaité. Le chemin le plus court, donc.
Je n'utilise pas non pluscar l'énoncé n'en fait pas mention, même si n'importe quelle machine pourrait le faire pour raccourcir ses calculs.
En effet la formule était stupide, je l'ai simplement testé sur un cas qui marchait et je n'ai pas pensé à vérifier les autres...
(n-k)*k ?
Peux-tu me donner le chemin le plus court pour obtenir A(4,2)=4? et la méthode que tu utilises pour construire le triangle de Pascal, il y en a bien une méthode. Tant que tu ne m'expliques pas ta méthode, je ne peux rien dire concernant les valeurs des A(n,k) que tu trouves.
deltab a écrit:Bonjour
Peux-tu me donner le chemin le plus court pour obtenir A(4,2)=4? et la méthode que tu utilises pour construire le triangle de Pascal?
Soit le triangle de pascal :
Pour obtenir le coefficient A(4,2), j'effectue le série d'additions suivantes :
(1,0) + (1,1) = 1 + 1 = 2 = (2,1)
(2,0) + (2,1) = 2 + 1 = 3 = (3,1)
(2,1) + (2,2) = 2 + 1 = 3 = (3,2)
(3,1) + (3,2) = 3 + 3 = 6 = (4,2)
Soit 4 additions en tout, A(4,2) = 4
Bonjour
La relation que j'ai donnée est erronée, des mêmes additions sont comptabilisée plus d'une fois.
On peut trouver des formules directes pour A(n,k)
La démonstration consiste à déterminer le nombre d'éléments calculés en partant de
calculés en partant de 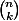 , chaque élément calculé
, chaque élément calculé  ne nécessite que l'addition de 2 éléments de la ligne
ne nécessite que l'addition de 2 éléments de la ligne 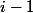 , les 2 éléments sont calculés si
, les 2 éléments sont calculés si  sinon un seul est calculé
sinon un seul est calculé 
Il semble bien que=k(n-k)) , elle bien vérifiée pour
, elle bien vérifiée pour  , on en déduit
, on en déduit =m^2) , relation vérifiée pour
, relation vérifiée pour ) et
et ) . Elle explique pourquoi aussi
. Elle explique pourquoi aussi =A(n,n-k)) .
.
La démonstration, il me semble, n'est pas difficile a faire, mais longue à rédiger. Je vais m'attaquer au cas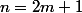 et
et  .
.
Trapnest a écrit:De même, pour obtenir le coefficient A(6,5), j'effectue le série d'additions suivantes :
(1,0) + (1,1) = 1 + 1 = 2 = (2,1)
(2,1) + (2,2) = 2 + 1 = 3 = (3,2)
(3,2) + (3,3) = 3 + 1 = 4 = (4,3)
(4,3) + (4,4) = 4 + 1 = 5 = (5,4)
(5,4) + (5,5) = 5 + 1 = 6 = (6,5)
Soit 4 additions en tout, A(6,5) = 5
La relation que j'ai donnée est erronée, des mêmes additions sont comptabilisée plus d'une fois.
On peut trouver des formules directes pour A(n,k)
La démonstration consiste à déterminer le nombre d'éléments
Il semble bien que
La démonstration, il me semble, n'est pas difficile a faire, mais longue à rédiger. Je vais m'attaquer au cas
Bonjour
Vous m"excuserez pour la présentation.
On fait le décompte des éléments calculés utilisés pour calculer
calculés utilisés pour calculer 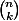 en remontant en remontant l'algorithme à partir de
en remontant en remontant l'algorithme à partir de 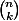
je traite ici le et
et 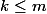 .
.
Ligne élément.
élément.
Ligne éléments
éléments
Ligne élément.
élément.
...............................
Ligne éléments
éléments
...............................
Ligne\quad \quad \quad \quad \quad \quad:{n-k+1 \choose 1},{n-k+1 \choose 2},\cdots,{n-k+1 \choose k}\quad \quad \quad \quad \quad \quad \quad \quad k) éléments
éléments
Ligne éléments ,
éléments ,
Ligne\quad \quad \quad \quad \quad \quad : {n-(k+1) \choose 1},{n-(k+1) \choose 2},\cdots,{n-(k+1) \choose k}\quad \quad \quad \quad) k éléments
k éléments
....................
Ligne éléments.
éléments.
Ligne éléments.
éléments.
Ligne éléments.
éléments.
...............................
Ligne éléments
éléments
.........................................
Ligne éléments.
éléments.
De la ligne à la ligne
à la ligne }{2}) éléments
éléments
De la ligne+1) à la ligne
à la ligne +n-2k-1:\quad \quad \quad k(n-2k-1)) éléments
éléments
De la ligne) à la ligne
à la ligne }{2}) éléments
éléments
Total:=\dfrac{k(k+1)}{2}+\dfrac{k(k+1)}{2})+k(n-2k-1)=k(n-k))
La relation=k(n-k))) reste valable si
reste valable si 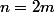 et
et 
Si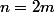 et
et 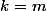
De la ligne à la ligne
à la ligne }{2}) éléments.
éléments.
De la ligne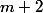 à la ligne
à la ligne }{2}) éléments.
éléments.
alors=\dfrac{m(m+1)}{2}+\dfrac{m(m-1)}{2}= m^2)
La même démarche sera utilisée pour)
Dans tous les cas , les éléments calculés utilisés forment un parallélogramme dont 2 sommets opposés sont
calculés utilisés forment un parallélogramme dont 2 sommets opposés sont  et
et 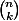 .
.
Vous m"excuserez pour la présentation.
On fait le décompte des éléments
je traite ici le
Ligne
Ligne
Ligne
...............................
Ligne
...............................
Ligne
Ligne
Ligne
....................
Ligne
Ligne
Ligne
...............................
Ligne
.........................................
Ligne
De la ligne
De la ligne
De la ligne
Total:
La relation
Si
De la ligne
De la ligne
alors
La même démarche sera utilisée pour
Dans tous les cas , les éléments
Bonsoir.
Il y a une démonstration plus rapide qui tient compte de la remarque suivante: si un élément calculé est utilisé pour le calcul de
est utilisé pour le calcul de 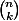 , tous les éléments de la colonne
, tous les éléments de la colonne  situés au dessus de
situés au dessus de  sont utilisés pour le calcul de {n \choose k}, élément diagonal non compris puisque non calculé. Les colonnes utilisées sont
sont utilisés pour le calcul de {n \choose k}, élément diagonal non compris puisque non calculé. Les colonnes utilisées sont  donc
donc  colonnes, leur plus bas élément suivent la diagonale passant par
colonnes, leur plus bas élément suivent la diagonale passant par 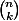 et parallèle à la diagonale principale, les colonnes utilisées comportent donc le même nombre d'éléments utilisés et celui-ci est égal à celui de la colonne
et parallèle à la diagonale principale, les colonnes utilisées comportent donc le même nombre d'éléments utilisés et celui-ci est égal à celui de la colonne  . Comme on a toujours
. Comme on a toujours 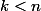 pour les éléments calculés, l'élément diagonal est alors
pour les éléments calculés, l'élément diagonal est alors  et le nombre d'éléments de la colonne
et le nombre d'éléments de la colonne  correspond aux lignes
correspond aux lignes  donc
donc 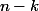 lignes et finalement on retrouve
lignes et finalement on retrouve =k(n-k)) .
.
Trapnest a écrit:Merci pour ce raisonnement, c'est maintenant clair :we:
Il y a une démonstration plus rapide qui tient compte de la remarque suivante: si un élément calculé
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
