Raisonnement par récurence

[Vados]

Bonsoir à tous j'aurai besoin de votre aide

On considère la suite (Un) définie pour tout n de N par :

U0 = 3 et Un+1 = (4Un-2) / Un + 1

1) Soit Un la fonction définie sur [1;+oo[ par f(x) = (4x -2) /(x+ 1)

a) Etudier les variations de f sur [1; +oo[
b) En déduire que pour tout x de [1; +oo[, f(x) est supérieur ou égal à 1

2) Démontrer par récurrence que, pour tout entier naturel n, Un est supérieur ou égal à 1.

3) Démontrer par récurrence que la suite (Un) est décroissante.

Où j'en suis

1) Il faut faire la dérivé ce qui donne f'(x) = 6/(x+1)² mais la je bloque car je ne sais plus si je dois dérivé le dénominateur et le numérateur séparément ce qui donnerai comme dérivé 4

[bab21]

Bonsoir,

f est de la forme u/v, il faut donc utiliser la formule f'=(u'v-v'u)/v² ce qui donne bien 6/(x+1)²

f' est donc positive sur intervalle, donc f est croissante

[alhazen]

Bonjour,

Tout d'abord on peut remarquer que (4x -2) /(x+ 1) peut se reecrire
=(4x+4)/(x+1) -6/(x+1)
= 4 -6/(x+1)

Comme -6/(x+1) est croissante sur [+1,+oo[ (remarquez que j'ai inclus le "-"), on a que 4-6/(x+1) est croissante aussi, car 4 est positif.

En consequence, sa plus petite valeur sera atteinte sur la borne inferieure de son domaine (en l'occurence, 1, avec f(x) = 1) et donc, toutes les valeurs sur [+1,oo[ seront superieures ou egales a 1.

[Vados]

Pour l'instant j'essaie de relire vos réponses , vous avez été tout les deux bien sympathique de m'apporter une réponse , mais j'aimerais que vous m'aidiez pour la prochaine question s'il vous plaît aussi :)

[bab21]

Pour l'instant j'essaie de relire vos réponses , vous avez été tout les deux bien sympathique de m'apporter une réponse , mais j'aimerais que vous m'aidiez pour la prochaine question s'il vous plaît aussi

Pour la question 2.
On remarque que Un+1 = (4Un-2) / Un + 1
Un+1 = (4Un+4-6)/(Un + 1)
Un+1 = 4 - 6/(Un + 1)

Initialisation: u0=3>1

Hérédité.
On suppose Un>1
=> Un + 1>2
=> 1/(Un + 1)6/(Un +1) -6/(Un + 1)>-3
=> 4-6/(Un + 1)>1
=> Un+1 >1

Il ne reste plus qu'à conclure

[alhazen]

Bonjour,

Pour la preuve par recurrence voici une solution:

element initial: uo >3 donc ca verifie la condition uo>1

Supposons que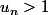 , il faut prouver que

On sait, par l'enonce, que a la forme

Par une reecriture similaire a celle de la premiere question, on a



Or, cette derniere expression est exactement celle de la question 1, avec u_n au lieu de x !. A cause de l'hypothese de recurrence, on sait que un > 1, et a cause de la premiere question, on sait que cette expression est strictement croissante. On a donc que toute l'expression est > 1, et donc que est superieure a 1, ce qui acheve la preuve

[Vados]

J'ai refais le calcul pour f'(x) et c'est bon ...
Vos deux méthodes semblent différentes , j'ai du mal à poursuivre sur la 1ère et je comprend pas la 2ème ...

[alhazen]

Bonjour vados,

je trouve au contraire que ma solution et celle de bab21 sont relativement similaires, presque les meme en fait (vu que son post date de 2h25 et le mien de 20h28, nous etions probablement en train d'ecrire en meme temps . Elles se basent toutes deux sur une reecriture de la'expression pour . La difference entre nos raisonnement c'est sur la fin: j'utilise le resultat de la premiere question sur la croissance de l'expression f(x). Au final c'est logique qu'ils aient pose les deux questions dans le meme bloc, si on peut resoudre la seconde avec l'aide de la premiere. mais comme bab21 le montre, ce n'est pas essentiel.

[bab21]

J'ai refais le calcul pour f'(x) et c'est bon ...
Vos deux méthodes semblent différentes , j'ai du mal à poursuivre sur la 1ère et je comprend pas la 2ème ...

Pour la question 1 a) Tu as f' positive, donc f est croissante.
pour la question 1 b) Tu as f croissante donc la plus petite valeur de f se trouve pour x =1. Or f(1)=1 donc f >1

[bab21]

Bonjour vados,

je trouve au contraire que ma solution et celle de bab21 sont relativement similaires, presque les meme en fait (vu que son post date de 2h25 et le mien de 20h28, nous etions probablement en train d'ecrire en meme temps . Elles se basent toutes deux sur une reecriture de la'expression pour . La difference entre nos raisonnement c'est sur la fin: j'utilise le resultat de la premiere question sur la croissance de l'expression f(x). Au final c'est logique qu'ils aient pose les deux questions dans le meme bloc, si on peut resoudre la seconde avec l'aide de la premiere. mais comme bab21 le montre, ce n'est pas essentiel.

Oui effectivement utiliser le résultat précédent semble plus logique au vu de l'énoncé :we:

[Vados]

Merci à vous je viens de comprendre ! Enfin vous avez validé ce que j'avais déjà compris ... et pour la prochaine question je ne sais pas comment m'y prendre non plus...

[Vados]

Et si je faisais tout simplement :

Je veut démontrer que Un>=1 donc
4un >= 4
4Un-2 > 2
4Un-2)/(Un+1) > 2/(Un+1)
donc Un +1 >= ou égale à 1 normalement

[bab21]

Et si je faisais tout simplement :

Je veut démontrer que Un>=1 donc
4un >= 4
4Un-2 > 2
4Un-2)/(Un+1) > 2/(Un+1)
donc Un +1 >= ou égale à 1 normalement

Non tu n'as pas le droit de dire si a>b et c>d alors a/c > b/d

Mais pour cette question alhazen et moi t'avons déjà répondu

[Vados]

Oui pardon j'ai mal ajusté le signe ! :O

C'est bizarre car vos réponses je ne l'ai avais pas vu ! autant pour moi ...

[Vados]

Oui je suis vraiment bête ! Mais pourquoi c'est plus simle de réaliser l'hérédité en modifiant Un+1?

[bab21]

Oui je suis vraiment bête ! Mais pourquoi c'est plus simle de réaliser l'hérédité en modifiant Un+1?

En utilisant l'écriture d'origine je ne suis pas sur que ce soit possible d'arriver au résultat.

Ce que tu as écrit (4Un-2)/(Un+1) > 2/(Un+1) ne permet pas de conclure Un +1 >= ou égale à 1 normalement. Car si un+1>2 cela peut être 4 et 2/42 et un + 1 >2 tu ne peux pas dire (4Un-2)/(un + 1)>1

[Vados]

D'accord très bien j'ai bien compris cette fois... C'est bien plus clair avec vous qu'avec certains profs..
Et du coup pour démontrer que la suite est décroissante , je fais Un+1 - Un ?

[bab21]

D'accord très bien j'ai bien compris cette fois... C'est bien plus clair avec vous qu'avec certains profs..
Et du coup pour démontrer que la suite est décroissante , je fais Un+1 - Un ?

Il est marqué qu'il faut démontrer que Un est décroissante par récurrence.

Donc il faut supposer que Un+1Un+1 + 11/(Un+1 + 1)>1/(Un + 1)
=>-1/(Un+1 + 1)-6/(Un+1 + 1)4-6/(Un+1 + 1)Un+2<Un+1

Il ne reste plus qu'a conclure