Equation avec les fonctions racines
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Sep 2014, 21:01
par adamNIDO » 07 Sep 2014, 21:01
Bonjour,
voila le problème tout entier

j'ai besoin seulement aide a les deux dernières questions:
pour
la question (4) pour monter que

vérifier
)
on a

donc

devient

(mais je sais pas pourque t > au sense stric et pas large )
 Pour la question (5)
Pour la question (5)le discriminant de
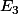
est

donc il y a deux solution distinct

or

on calcule dabord la valeur de

en fonction

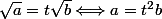
je suis bloqué la
Aidez-moi, s'il vous plait!
-
alegaxandra
- Membre Naturel
- Messages: 31
- Enregistré le: 08 Aoû 2014, 07:34
-
 par alegaxandra » 07 Sep 2014, 21:54
par alegaxandra » 07 Sep 2014, 21:54
Les deux solutions en t amènent à résoudre un système d'équations à deux inconnues en b et a. Calcule :
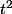
.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Sep 2014, 21:57
par adamNIDO » 07 Sep 2014, 21:57
alegaxandra a écrit:Les deux solutions en t amènent à résoudre un système d'équations à deux inconnues en b et a. Calcule
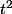
.
pourrait donner plus de details
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 07 Sep 2014, 22:24
par deltab » 07 Sep 2014, 22:24
Bonsoir.
adamNIDO a écrit:pourrait donner plus de details
Tu as donné finalement l'énoncé complet de l'exercice.
Pourquoi t>0? L'équation donnée est t-(1/t)=1
N'oublies pas les définitions de a et b en fonction de x.
PS: Le titre du post est erroné. Il s'agit de fonctions racines et non de fonctions puissance
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 08 Sep 2014, 08:26
par adamNIDO » 08 Sep 2014, 08:26
deltab a écrit:Bonsoir.
Tu as donné finalement l'énoncé complet de l'exercice.
Pourquoi

L'équation donnée est
=1)
N'oublies pas les définitions de a et b en fonction de

.
PS: Le titre du post est erroné. Il s'agit de fonctions racines et non de fonctions puissance
Bonjour,
Merci pour votre attention J'ai rectifié le problème du titre mais je suis encore entrain de trouver la solution de léquation en question par résoudre le System
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 08 Sep 2014, 11:07
par deltab » 08 Sep 2014, 11:07
Bonjour.
adamNIDO a écrit:Bonjour,
Merci pour votre attention J'ai rectifié le problème du titre mais je suis encore entrain de trouver la solution de léquation en question par résoudre le System
Pour 5) on a trouvé que

et on avait posé auparavant

avec

et

. On a alors:

d'où

........
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 08 Sep 2014, 11:39
par adamNIDO » 08 Sep 2014, 11:39
deltab a écrit:Bonjour.
Pour 5) on a trouvé que

et on avait posé auparavant

avec

et

. On a alors:

d'où

........
Bonjour.
oui je trouvé la solution sauf que

et ne vérifier pas léquation

merci beaucoup
-
alegaxandra
- Membre Naturel
- Messages: 31
- Enregistré le: 08 Aoû 2014, 07:34
-
 par alegaxandra » 08 Sep 2014, 12:03
par alegaxandra » 08 Sep 2014, 12:03
deltab a écrit:Bonjour.
Pour 5) on a trouvé que

et on avait posé auparavant

avec

et

. On a alors:

d'où

........
Oui, j'avais lu rapidement ce qui vient d'être complété. La solution pour t>0 en x donne la valeur de

-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 08 Sep 2014, 12:17
par adamNIDO » 08 Sep 2014, 12:17
alegaxandra a écrit:Oui, j'avais lu rapidement ce qui vient d'être complété. La solution pour t>0 en x donne la valeur de

merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités


L'équation donnée est
.