Convexité

[lopilu]

Bonsoir à tous.
Voilà, je viens de calculer la dérivée seconde d'une fonction, et on me demande de montrer que la fonction est convexe. En toute logique, je me dois de montrer que la dérivée seconde est positive sur l'intervalle considéré. Le hic, c'est que je ne sais pas comment m'y prendre après plusieurs tentatives...

Merci bien !

[deltab]

Bonsoir.

Bonsoir à tous.
Voilà, je viens de calculer la dérivée seconde d'une fonction, et on me demande de montrer que la fonction est convexe. En toute logique, je me dois de montrer que la dérivée seconde est positive sur l'intervalle considéré. Le hic, c'est que je ne sais pas comment m'y prendre après plusieurs tentatives...

Merci bien !

Calcules (ça va être une fonction rationnelle) et étudies si possible son signe, tu pourra peut-être avoir le signe de

[adrien69]

C'est quoi ta fonction de départ ? (épargne-nous un calcul de primitive odieux s'il te plaît)

[lopilu]

C'est quoi ta fonction de départ ? (épargne-nous un calcul de primitive odieux s'il te plaît)

Normalement il ne devrait pas y avoir de calcul de primitive... Ma fonction de départ était :
Définie sur par : sinon .
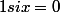
La première dérivée est :
La seconde dérivée, donnée dans le sujet est :
En gros il suffit donc de montrer que B(x) est positive, et le convexité vient toute seule...

[deltab]

Je corrige ma réponse en conséquence.
Calcules (ça va être une fonction rationnelle) et étudies si possible son signe, tu pourra peut-être avoir le signe de

[deltab]

Je corrige mon message en conséquence.
Calcules (ça va être une fonction rationnelle) et étudies si possible son signe, tu pourra peut-être avoir le signe de

[lopilu]

J'avais entrepris cela au début, mais autant pour moi j'avais fais une simple erreur de signe... Mortelle lorsqu'il s'agit de chercher le signe. Merci infiniment !

[chan79]

Normalement il ne devrait pas y avoir de calcul de primitive... Ma fonction de départ était :
Définie sur par : sinon .
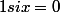
La première dérivée est :
La seconde dérivée, donnée dans le sujet est :
En gros il suffit donc de montrer que B(x) est positive, et le convexité vient toute seule...

B(0)=0
Si tu montres que B est croissante sur R+, c'est bon.
Encore un calcul de dérivée à faire

[Le Chat]

Bah, il suffit de montrer que , non? :hum:

[deltab]

Bah, il suffit de montrer que , non? :hum:

Tu as écrit "=>" qu'on peut confondre avec l'implication, il valait mieux écrire ">="

[mr_pyer]

Une autre méthode pour montrer la convexité de c'est remarquer que et de noter que est convexe quelque soit . Ça n'est pas la méthode la plus canonique je le conçois...

[Le Chat]

Tu as écrit "=>" qu'on peut confondre avec l'implication, il valait mieux écrire ">="

raaah mais oui mais oui