Limite

[lopilu]

Bonjour !
Je suis certain que cette limite n'est pas sorcier, mais ça fait une heure que j'y suis et j'ai essayé toutes les méthodes que je connaissais. La voici :

Merci beaucoup !

[adrien69]

Salut,

Le concept de développement limité, tu connais ? Et la décomposition en éléments simples ?

[lopilu]

Le décomposition en éléments simple ne mène à rien, et le développement limité n'est pas concluant... Après il se peut que je fasse des erreurs, le temps de se remettre dedans !

[adrien69]

Bien sûr que si ça mène à quelque chose. Surtout si tu fais les deux en même temps.

[lopilu]

En faisant un développement limité d'ordre 2 en 0, selon la méthode utilisée par notre professeur, je tombe sur un problème de négligeabilité. Voici la démonstration :

Les représentant les négligeabilités.
J'en arrive donc à la fin à :

Et il me faudrait en revanche des devant chaque epsilon. Suggestion(s) ?

[adrien69]

En faisant un développement limité d'ordre 2 en 0, selon la méthode utilisée par notre professeur, je tombe sur un problème de négligeabilité. Voici la démonstration :

Les représentant les négligeabilités.
J'en arrive donc à la fin à :

Et il me faudrait en revanche des devant chaque epsilon. Suggestion(s) ?

Eh ben ? Je ne vois pas pourquoi tu voudrais avoir quoi que ce soit en plus. T'as fini non ? Ça a quoi comme propriétés ?

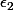
(y avait même pas besoin de la décomposition t'as vu ?)

[adrien69]

En fait avec la bouteille tu verras que pour la première partie, tu n'avais besoin que d'un DL d'ordre 1 alors que pour la seconde c'était bien un DL d'ordre 2 qu'il fallait. Et le coup de la décompo ça aide en ce que tu connais la limite de 1/(x+1) sans soucis.

Je te montre :




Et ça ça tend bien vers -1/2

[lopilu]

D'accord c'est bien plus clair maintenant !
Merci beaucoup en tout cas, j'ai tendance à beaucoup trop me prendre la tête avec les questions de rédaction...

[adrien69]

Comme tout le monde, ne t'en fais pas, ça viendra avec le temps.