Exo arithmétique svp

[Le Chat]

bonjour,

j'ai essayé toutes sortes de choses :help:

prouvez l'énoncé suivant:

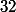
Si n'est pas divisible par , alors est pair.

des pistes??

merci

[zygomatique]

salut

donc par contraposée ::

si a est impair alors ....

[Le Chat]

salut

donc par contraposée ::

si a est impair alors ....

j'ai essayé par la contraposée, oui, mais je bloques :mur:

si a est impair, les 2 facteurs sont pairs et leur produit est pair...et alors?

[qelmcpc]

bah 32 = 2^5.
Si tu poses a = 2k + 1
alors tu developpes a² + 3. Tu factorises par 2^2.
De l'autre coté, tu développes et factorises par 2^3.
Au final, tu as bien que ton expression est divisible par 2^5, soit 32.

[chan79]

j'ai essayé par la contraposée, oui, mais je bloques :mur:

si a est impair, les 2 facteurs sont pairs et leur produit est pair...et alors?

si a est impair, alors a est de la forme 2p+1
il suffit de remplacer:
((2p+1)²+3)((2p+1)²+7)
Développe chaque grande parenthèse

[Le Chat]

si a est impair, alors a est de la forme 2p+1
il suffit de remplacer:
((2p+1)²+3)((2p+1)²+7)
Développe chaque grande parenthèse

Ça donne:

k e lN

On divise par 32 ;

enfin, on peut verifier que 3p + p^4 = p(3+p^3) est pair pour n'importe quel p e lN

e lN pour tout p e lN

donc, tous les a impairs (a=2p+1) rendent l'énoncé non-valide. Si l'énoncé est valide, alors a est pair puisque un entire est soit pair/impair...

CQFD?? :hein:

[chan79]

Ça donne:

k e lN

On divise par 32 ;

ça donne (4p²+4p+4)(4p²+4p+8)=16(p²+p+1)(p²+p+2)
Il faut observer les nombres dans les parenthèses

[Le Chat]

ça donne (4p²+4p+4)(4p²+4p+8)=16(p²+p+1)(p²+p+2)
Il faut observer les nombres dans les parenthèses

16(p²+p+1)(p²+p+2) = 16*2m où m e lN

= 32 m

[chan79]

16(p²+p+1)(p²+p+2) = 16*2m où m e lN

= 32 m

p²+p+1 et p²+p+2 sont consécutifs; l'un des deux est pair

[Le Chat]

tiens, je n'y avais pas pensé

merci messieurs :zen: