Un exercice sur la continuité

[nour2013]

salut
est ce que je peux avoir une reponse
exercice

soit f(x)=1 si x>0 ,f(x)=0 si x=0 ,f(x)=-1 si x<1
1)calculer valeur absolue (f(x)-f(0))
2)peut on rendre la quantité valeur absolue (f(x)-f(0)) aussi petite que l on veut ,en rapprochant x de 0

si possibles de me proposer des exemples qui m expose comment utiliser la définition de la continuité (avec epsilon et alpha)

merci

[Black Jack]

f(x) n'est pas correctement défini par : f(x)=1 si x>0 ,f(x)=0 si x=0 ,f(x)=-1 si x0 ,f(x)=0 si x=0 ,f(x)=-1 si x<0

Si c'est bien cela, alors :
|f(x) - f(0)| = 0 si x = 0
|f(x) - f(0)| = 1 si x différent de 0

:zen:

[nour2013]

salut oui c est vrai il ya une faute de frappe

f(x) défini par : f(x)=1 si x>0 ,f(x)=0 si x=0 ,f(x)=-1 si x<0


Si c'est bien cela, alors :
|f(x) - f(0)| = 0 si x = 0
|f(x) - f(0)| = 1 si x différent de 0

la suite svp
peut on rendre la quantité |f(x) - f(0)| aussi petite que l on veut en rapprochant x de 0

merci bien

[Shew]

salut oui c est vrai il ya une faute de frappe

f(x) défini par : f(x)=1 si x>0 ,f(x)=0 si x=0 ,f(x)=-1 si x<0


Si c'est bien cela, alors :
|f(x) - f(0)| = 0 si x = 0
|f(x) - f(0)| = 1 si x différent de 0

la suite svp
peut on rendre la quantité |f(x) - f(0)| aussi petite que l on veut en rapprochant x de 0

merci bien

On rearrange f(x) et f(0) quand on les sort de la valeur absolue en fonction de la valeur de x .

[nour2013]

salut
ce n est pas tés claire si possible de m expliquer d avantage
merci

[Black Jack]

salut oui c est vrai il ya une faute de frappe

f(x) défini par : f(x)=1 si x>0 ,f(x)=0 si x=0 ,f(x)=-1 si x<0


Si c'est bien cela, alors :
|f(x) - f(0)| = 0 si x = 0
|f(x) - f(0)| = 1 si x différent de 0

la suite svp
peut on rendre la quantité |f(x) - f(0)| aussi petite que l on veut en rapprochant x de 0

merci bien

Pour toute valeur de x différente de 0 et donc , même en "rapprochant" x de 0 (sans que x soit égal à 0), on a |f(x) - f(0)| = 1.
Cela devrait répondre à ta question.

N'est ce pas évident ?

:zen:

[Shew]

salut
ce n est pas tés claire si possible de m expliquer d avantage
merci

Si x > 0 si x < 0

[MacManus]

Salut,

Même si f est définie en 0, f n'est pas continue en 0, car les limites de f en 0 à droite et à gauche sont différentes (il y a un saut en 0) :



Donc et f n'est pas continue en 0.

Définition de la continuité de f en 0:

, c'est-à-dire

On voit que si on choisit par exemple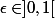 , alors l'implication ci-dessus n'est pas vérifiée, puisque si x différent de 0.

[paquito]

La définition de la continuité en 0 est:

, pour on aura , donc f n'est pas continue en 0;

c'est uniq uement pour te donner les définition, dans la pratique, on écrit différent de