équation complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 17 Aoû 2014, 17:11
par marco_seb » 17 Aoû 2014, 17:11
Bonsoir,
Je n'ai pas réussis à résoudre l'équation (z-1)^n = (z +1)^n.
Si quelqu'un pouvait m'aider, ce serait sympa.
Merci d'avance.
Marco.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 17 Aoû 2014, 17:19
par chan79 » 17 Aoû 2014, 17:19
marco_seb a écrit:Bonsoir,
Je n'ai pas réussis à résoudre l'équation (z-1)^n = (z +1)^n.
Si quelqu'un pouvait m'aider, ce serait sympa.
Merci d'avance.
Marco.
salut
^n=1)
Penser au cas n=0
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 17 Aoû 2014, 18:19
par marco_seb » 17 Aoû 2014, 18:19
Merci, ça fait 1.
et le reste(pour n=1 etc)?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 17 Aoû 2014, 18:29
par Ericovitchi » 17 Aoû 2014, 18:29
Merci, ça fait 1
:hein:
tu es devant des nombres complexes, si
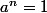
alors

k variant de 0 à n-1. ce qui te donne n racines de l'unité.
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 17 Aoû 2014, 18:34
par marco_seb » 17 Aoû 2014, 18:34
ok merci.
c'est vrai que 1 correspond à e^i2kpi sur le cercle!
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 17 Aoû 2014, 19:02
par marco_seb » 17 Aoû 2014, 19:02
il faut donc conclure en résolvant (z-1)/(z+1)==e^i2kpi/2, n'Est-ce pas?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 17 Aoû 2014, 19:22
par chan79 » 17 Aoû 2014, 19:22
marco_seb a écrit:il faut donc conclure en résolvant (z-1)/(z+1)==e^i2kpi/2, n'Est-ce pas?
sans doute une erreur de frappe:
(z-1)/(z+1)==e^i2kpi/
net si k=0 ?
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 17 Aoû 2014, 19:31
par marco_seb » 17 Aoû 2014, 19:31
oui c'est n et pas 2!
oublié de dire c'est pour n>0

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Aoû 2014, 08:33
par chan79 » 18 Aoû 2014, 08:33
marco_seb a écrit:oui c'est n et pas 2!
oublié de dire c'est pour n>0
Pour n=1, reprends l'équation de départ.
Pour n=6, combien de solutions ?
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 18 Aoû 2014, 10:58
par marco_seb » 18 Aoû 2014, 10:58
pour n=1, il n'y a pas de solutions!

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Aoû 2014, 12:44
par chan79 » 18 Aoû 2014, 12:44
marco_seb a écrit:pour n=1, il n'y a pas de solutions!
c'est bien ça
-
marco_seb
- Membre Naturel
- Messages: 47
- Enregistré le: 26 Mai 2013, 15:11
-
 par marco_seb » 18 Aoû 2014, 12:50
par marco_seb » 18 Aoû 2014, 12:50
cool merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
