Suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 14 Aoû 2014, 21:43
par marcopolo20 » 14 Aoû 2014, 21:43
Bonsoir,
https://mega.co.nz/#!mFYAFRQZ!JrqT3k4PVL8sObBBJAW5nEEUTEBycAMxLV235P0WUjE
Pour la 1), je trouves 2e^(-n/2)(-1+e^(1/2)) mais je n'arrive pas à répondre à la 2).
Merci de votre aide

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 14 Aoû 2014, 22:17
par Sake » 14 Aoû 2014, 22:17
Combien vaut u_{n+1} ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 00:44
par deltab » 15 Aoû 2014, 00:44
Bonjour
Qu'obtiens-tu si tu poses
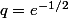
et
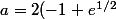)
?
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 16:18
par marcopolo20 » 15 Aoû 2014, 16:18
Sake a écrit:Combien vaut u_{n+1} ?
2e^(-n/2)(1-e^(1/2))
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 16:36
par marcopolo20 » 15 Aoû 2014, 16:36
deltab a écrit:Bonjour
Qu'obtiens-tu si tu poses
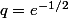
et
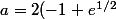)
?
Un = e^((-1/2)^n)*2(-1+e^(1/2))

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 15 Aoû 2014, 16:37
par Sake » 15 Aoû 2014, 16:37
marcopolo20 a écrit:2e^(-n/2)(1-e^(1/2))
Tu es sûr ???
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 16:41
par marcopolo20 » 15 Aoû 2014, 16:41
Sake a écrit:Tu es sûr ???
non, plutôt
2e^(-n/2)(1-e^(-1/2))

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 15 Aoû 2014, 16:47
par Sake » 15 Aoû 2014, 16:47
marcopolo20 a écrit:non, plutôt
2e^(-n/2)(1-e^(-1/2))
Oui mais c'est pas ça qui est intéressant...
On voit surtout que u_{n+1} = e^{-1/2}*u_n, et c'est juste assez
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 17:08
par deltab » 15 Aoû 2014, 17:08
Bonjour
marcopolo20 a écrit:Un = e^((-1/2)^n)*2(-1+e^(1/2))
Pourquoi n'as tu pas fait ce que je t'ai demandé?
Même avec l'erreur sur

, on a
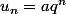
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 17:10
par marcopolo20 » 15 Aoû 2014, 17:10
Sake a écrit:Oui mais c'est pas ça qui est intéressant...
On voit surtout que u_{n+1} = e^{-1/2}*u_n, et c'est juste assez
Ah oui, merci. Je n'arrive pas à voir ce genre de chose.
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 17:24
par marcopolo20 » 15 Aoû 2014, 17:24
deltab a écrit:Bonjour
Pourquoi n'as tu pas fait ce que je t'ai demandé?
Même avec l'erreur sur

, on a
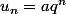
Mais c'est la même chose que ça Un = ((e^(-1/2))^n)*2(-1+e^(1/2)) (j'avais mal mit les parenthèses) mais je ne comprenais pas comment trouver à quoi correspondais q.

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 15 Aoû 2014, 18:23
par Sake » 15 Aoû 2014, 18:23
marcopolo20 a écrit:Ah oui, merci. Je n'arrive pas à voir ce genre de chose.
C'est que tu as mal appris ton cours. Une suite géométrique est définie par un premier terme et tout terme (sauf le premier) vaut une constante fois le terme précédent. Alors il faut calculer u_{n+1} et voir que c'est égal à k*u_n, tout simplement.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 18:43
par deltab » 15 Aoû 2014, 18:43
marcopolo20 a écrit:Mais c'est la même chose que ça Un = ((e^(-1/2))^n)*2(-1+e^(1/2)) (j'avais mal mit les parenthèses) mais je ne comprenais pas comment trouver à quoi correspondais q.
Je t'avais donné la valeur de

. Pour voir que

est le terme général d'une suite géométrique, c'est essayer de faire une identification entre l'expression de

et la forme

,
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
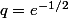 et
et 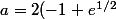) ?
?