Limite d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Aoû 2014, 21:33
par deltab » 14 Aoû 2014, 21:33
Bonsoir.
marcopolo20 a écrit:4) Question 5-a) Il suffit de montrer que
 \subset [1,\alpha])
.
oui mais je ne vois pas comment
Quelle est l'image d'un intervalle

par une fonction continue et monotone sur

?
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 14 Aoû 2014, 21:39
par marcopolo20 » 14 Aoû 2014, 21:39
deltab a écrit:Bonsoir.
Quelle est l'image d'un intervalle

par une fonction continue et monotone sur

?
[a;b] je penses
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 00:31
par deltab » 15 Aoû 2014, 00:31
Bonjour
marcopolo20 a écrit:[a;b] je penses
Vraiment!
=[0,1])
et non
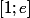
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 08:44
par marcopolo20 » 15 Aoû 2014, 08:44
deltab a écrit:Bonjour
Vraiment!
=[0,1])
et non
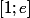
ok donc la réponse est simplement : g([1;alfa])=[g(1);g(alfa)]=[ln(3);alfa] car g est continue et monotone sur [-1/2;+infini] et donc sur [1;alfa] ; de plus Uo=1 donc Un C [1;alfa] car 1<ln(3)
Je n'arrive pas à répondre à la question de la question 5 d), je suppose qu'il faut s'aider de ce que l'on vient de montrer mais je ne vois pas comment.
Merci de votre aide
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 12:01
par deltab » 15 Aoû 2014, 12:01
Bonjour.
marcopolo20 a écrit:Je n'arrive pas à répondre à la question de la question 5 d), je suppose qu'il faut s'aider de ce que l'on vient de montrer mais je ne vois pas comment.
En t'aidant de la question 5.c), montre par récurrence que pour tout
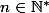
,
^n[U_0-\alpha|)
. (N'oublies pas
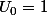
et

(donné dans l'énoncé.) Que peux-tu en déduire?
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 12:53
par marcopolo20 » 15 Aoû 2014, 12:53
deltab a écrit:Bonjour.
En t'aidant de la question 5.c), montre par récurrence que pour tout
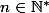
,
^n[U_0-\alpha|)
. (N'oublies pas
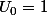
et

(donné dans l'énoncé.) Que peux-tu en déduire?
J'ai réussi merci
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 13:36
par marcopolo20 » 15 Aoû 2014, 13:36
deltab a écrit:Bonjour.
En t'aidant de la question 5.c), montre par récurrence que pour tout
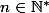
,
^n[U_0-\alpha|)
. (N'oublies pas
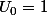
et

(donné dans l'énoncé.) Que peux-tu en déduire?
Je ne vois pas ce que l'on peut en déduire, mais je ne comprend pas vraiment à quoi correspond le rang, ni à quelle valeur approchée on commence.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 16:11
par deltab » 15 Aoû 2014, 16:11
Bonjour.
marcopolo20 a écrit:Je ne vois pas ce que l'on peut en déduire, mais je ne comprend pas vraiment à quoi correspond le rang, ni à quelle valeur approchée on commence.
As-tu montré que
^n[U_0-\alpha|)
?
Si
OUI, ce n'est pour rien que j'ai appelé la valeur de

et la valeur approchée de

.
Si
NON, commences par le montrer (par récurrence)!!
-
marcopolo20
- Membre Relatif
- Messages: 145
- Enregistré le: 10 Fév 2012, 15:57
-
 par marcopolo20 » 15 Aoû 2014, 17:02
par marcopolo20 » 15 Aoû 2014, 17:02
deltab a écrit:Bonjour.
As-tu montré que
^n[U_0-\alpha|)
?
Si
OUI, ce n'est pour rien que j'ai appelé la valeur de

et la valeur approchée de

.
Si
NON, commences par le montrer (par récurrence)!!
Oui, je l'ai montré. Donc
^n*0.26)
mais je ne remarque rien.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 18:55
par deltab » 15 Aoû 2014, 18:55
marcopolo20 a écrit:Oui, je l'ai montré. Donc
^n*0.26)
mais je ne remarque rien.
et
|0.26|<= 1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
.
et non
,
. (N'oublies pas
et
(donné dans l'énoncé.) Que peux-tu en déduire?