Bonjour,
J'ai une fonction f de plusieurs variables dont les dérivées d'ordre 1, 2 et 3 en un point sont nulles.
Comment, en regardant la dérivée d'ordre 4 en ce point, je peux déterminer si cette fonction admet un extrémum local?
Dans le cas où la dérivée première est nulle, et la dérivée seconde non nulle, je sais qu'il faut regarder si la dérivée seconde est définie.
Y a-t-il une généralisation de cette idée aux ordres supérieurs?
Test d'extrémum au 4ème ordre
6 messages
- Page 1 sur 1
Avec f'(a) = f''(a) = f'''(a) = 0
Supposons f'''' > 0 (juste) à gauche du point d'abscisse a ---> f''' est donc croissante à gauche du point et donc f''' < 0 à gauche du point ---> f'' est décroissante à gauche du point ---> f'' > 0 à gauche du point ---> f' est croissante à gauche du point ---> f' < 0 à gauche du point.
Donc f'''' > 0 à gauche du point ---> f' < 0 à gauche du point et donc f est décroissante à gauche du point.
Raisonnement analogue ---> f'''' < 0 à gauche du point ---> f' > 0 à gauche du point et donc f est croissante à gauche du point.
*****
Supposons f'''' > 0 (juste) à droite du point ---> f''' est donc croissante à droite du point et donc f''' > 0 à droite du point ---> f'' est croissante à droite du point ---> f'' > 0 à droite du point ---> f' est croissante à droite du point ---> f' > 0 à gauche du point.
Donc f'''' > 0 à droite du point ---> f' > 0 à droite du point et donc f est croissante à droite du point.
Raisonnement analogue ---> f'''' < 0 à droite du point ---> f' < 0 à droite du point et donc f est décroissante à droite du point.
*****
Donc, si je ne me suis pas planté :
Avec f'(a) = f''(a) = f'''(a) = 0
Si f'''' > 0 à gauche et à droite du point d'abscisse a, il y a un minimum local
Si f'''' < 0 à gauche et à droite du point d'abscisse a, il y a un maximum local
Si f'''' change de signe en passant de gauche à droite de x = a ---> pas d'extremums.
A vérifier ... bien entendu.
:zen:
Supposons f'''' > 0 (juste) à gauche du point d'abscisse a ---> f''' est donc croissante à gauche du point et donc f''' < 0 à gauche du point ---> f'' est décroissante à gauche du point ---> f'' > 0 à gauche du point ---> f' est croissante à gauche du point ---> f' < 0 à gauche du point.
Donc f'''' > 0 à gauche du point ---> f' < 0 à gauche du point et donc f est décroissante à gauche du point.
Raisonnement analogue ---> f'''' < 0 à gauche du point ---> f' > 0 à gauche du point et donc f est croissante à gauche du point.
*****
Supposons f'''' > 0 (juste) à droite du point ---> f''' est donc croissante à droite du point et donc f''' > 0 à droite du point ---> f'' est croissante à droite du point ---> f'' > 0 à droite du point ---> f' est croissante à droite du point ---> f' > 0 à gauche du point.
Donc f'''' > 0 à droite du point ---> f' > 0 à droite du point et donc f est croissante à droite du point.
Raisonnement analogue ---> f'''' < 0 à droite du point ---> f' < 0 à droite du point et donc f est décroissante à droite du point.
*****
Donc, si je ne me suis pas planté :
Avec f'(a) = f''(a) = f'''(a) = 0
Si f'''' > 0 à gauche et à droite du point d'abscisse a, il y a un minimum local
Si f'''' < 0 à gauche et à droite du point d'abscisse a, il y a un maximum local
Si f'''' change de signe en passant de gauche à droite de x = a ---> pas d'extremums.
A vérifier ... bien entendu.
:zen:
Je pense que cette solution ne fonctionne pas mais je n'en suis pas sûr.
La possibilité d'avoir un critère simple d'extremum, dans le cas d'une fonction f vérifiant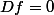 et
et 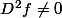 , c'est-à-dire de n'avoir à regarder que les dérivées partielles, repose selon moi sur la proposition d'algèbre suivante:
, c'est-à-dire de n'avoir à regarder que les dérivées partielles, repose selon moi sur la proposition d'algèbre suivante:
Une forme bilinéaire symétrique est positive si et seulement si la forme quadratique associée est positive pour tous les éléments d'une base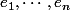 .
.
Ce résultat est-il valable en dimension supérieure?
Une forme (2n)-linéaire symétrique est-elle positive si et seulement si elle donne des valeurs positives quand on l'applique aux 2n-uplets:, \cdots (e_n, \cdots, e_n))
Quelqu'un peut-il confirmer ou infirmer cela?
La possibilité d'avoir un critère simple d'extremum, dans le cas d'une fonction f vérifiant
Une forme bilinéaire symétrique est positive si et seulement si la forme quadratique associée est positive pour tous les éléments d'une base
Ce résultat est-il valable en dimension supérieure?
Une forme (2n)-linéaire symétrique est-elle positive si et seulement si elle donne des valeurs positives quand on l'applique aux 2n-uplets:
Quelqu'un peut-il confirmer ou infirmer cela?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
