Convergence d'une simple série.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 10 Aoû 2014, 14:53
par Mikihisa » 10 Aoû 2014, 14:53
Bonjour ! Je doit étudier la convergence de la série suivante, suivant les valeur es de a dans ]0;+oo[
}))
Oe je sais elle fait peur mais en fait ça se simplifie très bien en prenant
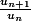
J'ai démontrer dans les question précédente le critère de Raabe-Duahmel, ainsi que d'autres critère sur un+1/un mais je n'arrive pas a conclure cette série :/.
J'ai ici
}{ln(n+1+a)})
On peut se ramener a du n en faisant un/un-1 (vn=un-1) pour simplifier l'expression mais je ne vois toujours pas comment conclure :/ des idée ?
Cordialement
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 10 Aoû 2014, 17:49
par deltab » 10 Aoû 2014, 17:49
Bonjour
Mikihisa a écrit:J'ai ici
}{ln(n+1+a)})
As-tu vu le critère qui consiste non pas à comparer

et

mais les rapports
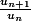
et

.
Il me semble que la série diverge pour tout
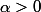
et même pour
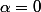
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Aoû 2014, 18:39
par Razes » 10 Aoû 2014, 18:39
Tu as oublié des termes:
}{ln(n+1+a)}\frac{ln(n+a)}{ln(n)})
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Aoû 2014, 18:51
par Razes » 10 Aoû 2014, 18:51
Procéder par DL en utilisant
 = x-\frac{x^2}2+\frac{x^3}3-\cdots+(-1)^{(n-1)}\frac{x^{n}}n+o(x^{n}))
et
=\ln (n)+\ln (1+\frac{b}{n}))
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 10 Aoû 2014, 19:10
par Mikihisa » 10 Aoû 2014, 19:10
Le terme dont tu parles n'est pas annuler vu qu'il apparaît dans les 2 produit ?
Sinon oui j'était parti sur ce dl la mais j'arrivais pas a conclure :/ après j'ai pris le dl a l'ordre 2 peut être faut-il le prendre a l'ordre n jvais voir, mais tu es sur que j'ai oublier des terme ??
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 12 Aoû 2014, 18:00
par deltab » 12 Aoû 2014, 18:00
@ Mikihisa
Juste avoir une idée, la nature de la série pour
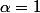
.
Maintenant grâce à un logiciel de tracé de courbes, j'ai pu voir que la fonction
}{\ln(x) \ln(x+2)})
tendait vers 1 en décroisant et en "déduire" que

où

et en conclure que
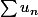
diverge.
Mais tout ceci n'est pas une démonstrationFais la même pour

-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Aoû 2014, 19:32
par cuati » 13 Aoû 2014, 19:32
Bonsoir,
sauf erreur de ma part, en posant
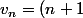\ln^a(n+1)u_n)
, on arrive à montrer (DL d'ordre 2) que
)
.
Donc la série de t.g.
)
converge.
Donc la suite

converge vers une limite non nulle

.
Donc
\ln^a(n+1)}\sim\frac{L}{n\ln^a(n)})
.
La série de t.g.

converge donc si et seulement si
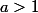
(série de Bertrand).
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 14 Aoû 2014, 11:26
par Mikihisa » 14 Aoû 2014, 11:26
Oui c'est vraiment pas mal. Par contre je n'ai pas capter le passage a ln(vn/vn-1).
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Aoû 2014, 12:44
par deltab » 14 Aoû 2014, 12:44
Bonjour
Mikihisa a écrit:Oui c'est vraiment pas mal. Par contre je n'ai pas capter le passage a ln(vn/vn-1).
C'est juste l'équivalence au voisinage de

:
 \sim u.)
Ce que je n'ai compris c'est plutôt comment cuati a obtenu ce DL?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 14 Aoû 2014, 14:13
par cuati » 14 Aoû 2014, 14:13
Bonjour,
avec
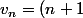\ln^a(n+1)u_n)
, on a :
1)\left(\frac{\ln(n+1)}{\ln(n)}\right)^a\left(1-\frac{1}{n}\right)\frac{\ln(n)}{\ln(n+a)}=\boxed{ \left(1-\frac{1}{n^2}\right)\left(\frac{\ln(n+1)}{\ln(n)} \right)^a\frac{\ln(n)}{\ln(n+a)}})
J'utilise ensuite dans 2) et 3) les DL du type suivant pour avoir un développement des deux derniers facteurs de

:
=x-\frac{x^2}{2}+...)
et

:
2)}{\ln(n+a)}=\frac{1}{1+\frac{\ln(1+ \frac{a}{n} )}{\ln(n)}}=\frac{1}{1+ \frac{a}{n\ln(n)}- \frac{a^2}{2n^2\ln(n)}+o\left(\frac{1}{n^2\ln(n)} \right)}= 1-\frac{a}{n\ln(n)}+\frac{a^2}{2n^2\ln(n)}+o\left( \frac{1}{n^2\ln(n)} \right))
Ce n'est pas évident mais dans la dernière égalité, on pourrait croire que c'est en fait un
} \right))
mais si on pousse le DL à l'ordre 2 on se rend compte que le dernier terme est en
}=o\left( \frac{1}{n^2\ln(n)} \right))
Donc :
}{\ln(n+a)}=\boxed{1-\frac{a}{n\ln(n)}+o\left( \frac{1}{n^2} \right)})
puisque
}=o\left( \frac{1}{n^2} \right)) 3) même méthode qu'au 2)
3) même méthode qu'au 2)Cette fois on utilise en plus un DL du type
^\alpha=1+\alpha x...)
}{\ln(n)} \right)^a=\left(1+\frac{\ln(1+ \frac{1}{n})}{\ln(n)} \right)^a=\left(1+ \frac{1}{n\ln(n)} -\frac{1}{2n^2\ln(n)}+o\left( \frac{1}{n^2\ln(n)}\right)\right)^a=\boxed{1+\frac{a}{n \ln(n) }+o\left( \frac{1}{n^2} \right)}) 4)
4) Finalement:
\left( 1+\frac{a}{n \ln(n) }+o\left( \frac{1}{n^2} \right) \right)\left( 1-\frac{a}{n\ln(n)}+o\left( \frac{1}{n^2} \right) \right)=\left(1-\frac{1}{n^2}\right)\left(1+o\left( \frac{1}{n^2} \right)\right)=\boxed{1-\frac{1}{n^2}+o\left( \frac{1}{n^2}\right)}) 5)
5) Voir mon premier post...
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Aoû 2014, 14:29
par deltab » 14 Aoû 2014, 14:29
@cuati
Merci des détails.
L'étape
1)\left(\frac{\ln(n+1)}{\ln(n)}\right)^a\left(1-\frac{1}{n}\right)\frac{\ln(n)}{\ln(n+a)}=\boxed{ \left(1-\frac{1}{n^2}\right)\left(\frac{\ln(n+1)}{\ln(n)} \right)^a\frac{\ln(n)}{\ln(n+a)}})
n'était-elle pas suffisante pour conclure?
\left(\frac{\ln(n+1)}{\ln(n)} \right)^a\frac{\ln(n)}{\ln(n+a)}}\sim 1-\frac{1}{n^2}{)
Le facteur
}{\ln(n)} \right)^a \frac{\ln(n)}{\ln(n+a)})
tend bien vers 1 quand n tend vers

.
Il y a peut-être une erreur dans l'expression de

.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 14 Aoû 2014, 16:30
par cuati » 14 Aoû 2014, 16:30
D'accord avec ta première remarque, j'aurai pu conclure plus vite...
'deltab' a écrit:Il y a peut-être une erreur dans l'expression de

.
Peut être, je n'ai pas remarqué...
'deltab' a écrit:De plus quel est le lien entre le a en exposant dans

el le a qui figure
Tu as terminé ta phrase ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 14 Aoû 2014, 20:27
par deltab » 14 Aoû 2014, 20:27
Bonjour.
cuati a écrit:D'accord avec ta première remarque, j'aurai pu conclure plus vite...
Peut être, je n'ai pas remarqué...
Tu as terminé ta phrase ?
J'ai voulu faire une remarque que j'ai laissé tomber et dont j'ai oublié de supprimer le début.
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 14 Aoû 2014, 21:05
par cuati » 14 Aoû 2014, 21:05
deltab a écrit:Bonjour.
J'ai voulu faire une remarque que j'ai laissé tomber et dont j'ai oublié de supprimer le début.
OK,
je ne vois pas d'erreur dans l'expression de

-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 15 Aoû 2014, 09:24
par cuati » 15 Aoû 2014, 09:24
deltab a écrit:L'étape
1)\left(\frac{\ln(n+1)}{\ln(n)}\right)^a\left(1-\frac{1}{n}\right)\frac{\ln(n)}{\ln(n+a)}=\boxed{ \left(1-\frac{1}{n^2}\right)\left(\frac{\ln(n+1)}{\ln(n)} \right)^a\frac{\ln(n)}{\ln(n+a)}})
n'était-elle pas suffisante pour conclure?
\left(\frac{\ln(n+1)}{\ln(n)} \right)^a\frac{\ln(n)}{\ln(n+a)}}\sim 1-\frac{1}{n^2})
Finalement non, cette étape n'est pas du tout suffisante pour conclure !
Ce n'est pas parce que deux suites sont équivalentes que leur log le sont aussi.
Contre-exemple :

mais
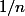
n'est pas équivalent à
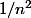
. Il faut avoir un DL pour pouvoir prendre le log...
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 15 Aoû 2014, 12:27
par Mikihisa » 15 Aoû 2014, 12:27
deltab a écrit:Bonjour
C'est juste l'équivalence au voisinage de

:
 \sim u.)
Ce que je n'ai compris c'est plutôt comment cuati a obtenu ce DL?
Donc on aurait
 =_{\infty} ln(1-\frac{1}{n^2}+o(\frac{1}{n^2}))=_{\infty} -\frac{1}{n^2}+o(\frac{1}{n^2})+o(-\frac{1}{n^2}+o(\frac{1}{n^2})))
? Et
 = -\sum \frac{1}{n^2} + \sum o(\frac{1}{n^2}) = -\sum \frac{1}{n^2}+o(\frac{1}{n^2}))
qui converge
Pas: j'ai oublier des terme mais les sommes des o sont des o donc au final on a le résultat c'est bon j'ai piger ^^
J'avais juste pas penser a ton vn vraiment bien jouer !
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 17:02
par deltab » 15 Aoû 2014, 17:02
Bonjour.
cuati a écrit:Donc la série de t.g.
)
converge.
Donc la suite

converge vers une limite non nulle

.
La série de t.g.
)
converge donc
 \to 0)
et donc encore

et ça, on le sait déjà
)
et on n'a aucune raison de conclure que


-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 15 Aoû 2014, 17:21
par cuati » 15 Aoû 2014, 17:21
deltab a écrit:Bonjour.
La série de t.g.
)
converge donc
 \to 0)
et donc encore

et ça, on le sait déjà
)
et on n'a aucune raison de conclure que


Je te rappelle que la
série de t.g.
)
est télescopique ! Autrement dit :
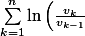=\ln(v_n)-\ln(v_1))
.
Dire que la série converge revient donc à dire que la suite
)
converge vers une limite

et que donc la suite

converge vers une limite

-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 15 Aoû 2014, 18:47
par deltab » 15 Aoû 2014, 18:47
cuati a écrit:Je te rappelle que la
série de t.g.
)
est télescopique ! Autrement dit :
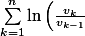=\ln(v_n)-\ln(v_1))
.
Dire que la série converge revient donc à dire que la suite
)
converge vers une limite

et que donc la suite

converge vers une limite

Merci pour les précisions
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
