Question

par **JaafarAitraf** » 01 Aoû 2014, 22:35

Qu'est ce que signifie P==>Q ? En formules mathématiques et en langues svp

par **titine** » 02 Aoû 2014, 08:05

JaafarAitraf a écrit:Qu'est ce que signifie P==>Q ? En formules mathématiques et en langues svp

Ça veut dire que la propriété P entraine la propriété Q. C'est à dire que si la propriété P est vraie alors la propriété Q est vraie.
Exemple :
P : ABC est un triangle rectangle en A
Q : BC² = AB² + AC²
On a P entraine Q.

par **Sake** » 02 Aoû 2014, 08:37

Si Martine a pas été sage, alors le Père-Noël ne passera pas :

Martine pas sage ==> Père-Noël ne passera pas ("Martine pas sage implique que le P-N ne passera pas...")

Si Titine ne t'avait pas expliqué ce qu'est l'implication, tu ne saurais pas ce que c'est :

Titine ne t'a pas expliqué l'implication ==> Tu ne sais toujours pas ce que c'est.

Mais alors la contraposée est vraie (par définition) : Tu sais ce qu'est l'implication car Titine t'a expliqué ce que c'est (Si tu sais ce qu'est l'implication, alors Titine te l'a expliqué, dans un cas idéal où tu n'aurais demandé à personne d'autre).

par **zygomatique** » 02 Aoû 2014, 10:09

titine a écrit:Ça veut dire que la propriété P entraine la propriété Q. C'est à dire que si la propriété P est vraie alors la propriété Q est vraie.
Exemple :
P : ABC est un triangle rectangle en A
Q : BC² = AB² + AC²
On a P entraine Q.

salut

pour expliquer l'implication il est peu judicieux de prendre l'exemple du théorème de Pythagore qui est une équivalence

car (A => B) (B => A) (non A => non B) (non B => non A)

un exemple plus simple est :

si n est multiple de 4 alors n est pair

par **Mikihisa** » 02 Aoû 2014, 10:59

1+1=3 => x^2+1=0 a des solutions dans R

Si si c'est vrai je vous assure :mur:

par **paquito** » 02 Aoû 2014, 13:05

Bonjour,

je tiens à dire que dans toute rédaction, il vaut mieux éviter l'implication, sauf si c'est pour citer un théorème, sinon on écrit n'importe quoi.

Un élève qui commence sa démonstration par: " si ABC est rectangle en A" alors qu'il faut démontrer que ABC est rectangle enA, pourra toujours écrire deux pages de calcul, il n'aura rien démontré!

De même : n multiple de 4 => n multiple de 2 ne démontre rien! C'est confondre "=>" et "donc", ce qui n'est pas du tout la même chose et on ne saura jamais si n est multiple de 2.

Ce qu'il faut appliquer c'est:"(p et p=>q)=>q" ce qui est un peu lourd.

Donc les démonstrations comportant => en dehors du cas où l'on cite un théorème sont toutes fausses! Bizarrement, l'équivalence est bien plus simple à manipuler.

J'ai oublier de parler du raisonnement par récurrence où il y a une implication à démontrer et non pas à utiliser, mais là encore c'est dangereux puisqu'on peut l'écrire:

et qu'il faut éviter d'écrire supposons que

d'une part et que l'implication peut être vraie alors que

est toujours fausse.

Donc puisqu'on ne fait plus de logique, évitons d'utiliser une notion aussi délicate.

par **beagle** » 02 Aoû 2014, 14:09

Ben pour ètre honnète vous (zygomatique et paquito) me faites peur.
Et heureusement que je n'ai pas rencontré cette rigueur appliquée avec rigidité,
je crois que je me serai barré ailleurs.
ouh la la.
certes pour bien se comprendre il faut utiliser les bons termes, mais je suis pour ètre cool sur les excès de langage, implique et donc...
Rien compris sur la récurrence, l'hérédité peut tout à fait étre faux implique faux, c'est bien l'initialisation qui fait la différence dans ce cas.

Faites peur les gars!

par **zygomatique** » 02 Aoû 2014, 14:15

Un élève qui commence sa démonstration par: " si ABC est rectangle en A" alors qu'il faut démontrer que ABC est rectangle enA, pourra toujours écrire deux pages de calcul, il n'aura rien démontré!

malheureusement ce que font beaucoup d'élèves de 1e et Term S ....

quant au reste ... certes oui ....

mais bon il est "évident" que quand on veut montrer Q et que l'on sait que P => Q est vraie il faut montrer P

ainsi l'implication "n est multiple de 4 => n est multiple de 2" est vraie ...

si je prouve que n est multiple de 4 alors je sais qu'il est multiple de 2 ...

c'est suffisant ... mais pas nécessaire puisque n = 6 est multiple de 2 et pas de 4 ...

:lol3:

et justement la récurrence c'est montrer qu'une implication est vraie ... tu as tout à fait raison

ensuite l'initialisation permet d'avoir P et (P => Q) vraie .... ce qui permet de conclure que Q est vraie ...

par **zygomatique** » 02 Aoû 2014, 14:17

beagle a écrit:Ben pour ètre honnète vous (zygomatique et paquito) me faites peur.
Et heureusement que je n'ai pas rencontré cette rigueur appliquée avec rigidité,
je crois que je me serai barré ailleurs.
ouh la la.
certes pour bien se comprendre il faut utiliser les bons termes, mais je suis pour ètre cool sur les excès de langage, implique et donc...
Rien compris sur la récurrence, l'hérédité peut tout à fait étre faux implique faux, c'est bien l'initialisation qui fait la différence dans ce cas.

Faites peur les gars!

et si ton garagiste te gonfle les pneus à peu près ....
et si ton garagiste te répare ta voiture à peu près ...
et si on te construit une maison à peu près ....

t'en penses quoi ?

MDR :mur:

par **beagle** » 02 Aoû 2014, 14:21

zygomatique a écrit:et si ton garagiste te gonfle les pneus à peu près ....
et si ton garagiste te répare ta voiture à peu près ...
et si on te construit une maison à peu près ....

t'en penses quoi ?

MDR :mur:

ben cela ne me fait pas MDR,
honnètement je n'ai pas souvenir de profs de maths psychorigide,
j'ai eu du bol???
Mais j'ai connu ce que vous racontez pour deux de mes trois prof de physiques au lycée,
ben je ne suis jamais revenu dans cette discipline.

par **beagle** » 02 Aoû 2014, 14:25

n multiple de 4 implique n multiple de 2

ben c'est simple, si dans l'énoncé il est dit d'une façon quelconque que n multiple de 4,
ben la démonstration est bonne,
vu que le jour où n n'est pas multiple de 4 s'appelle l'exercice suivant!

sur la récurrence, toujours rien compris de ce que vous cherchez à montrer, bien vous soyez deux personnes à écrire de façon rigoureuse, alors ...

par **beagle** » 02 Aoû 2014, 14:34

Pour si ABC triangle rectangle alors qu'on veut démontrer ABC triangle rectangle,
faudrait détailler un peu quels éléments de départ de l'énoncé
et quelle démarche a été faite
on part de ABC triangle rectangle pour aller d'implications en implications vers ABC triangle rectangle c'est cela??
si vous pouvez prendre des exemples ...

par **maylis1001** » 02 Aoû 2014, 14:36

bonjour je suis nouvelle et j'ai besoin d'aide :

comment passer de : d² = D² + ((x+(a/2))² à d = D racine 1 + ((x + a/2) / D ) ²

merci de me répondre

par **beagle** » 02 Aoû 2014, 15:04

Prenons un exemple.
on distribue le mème nombre de bonbons à Julie,Manon, Kevin et Karim.
Peut-on ranger les bonbons dans deux boites contenant le mème nombre de bonbons.

n multiple de 4 implique n multiple de deux
donc oui je peux ranger les bonbons dans deux boites.

Vous considérez cela une non démonstration,
alors qu'il ne s'agit que de sous-entendus non écrits,
l'élève n'écrivant pas n est bien multiple de 4 puisque chacun des 4 personnages a le mème nombre de bonbons,
donc un langage qui n'énonce pas tout, un raccourci.

mais alors on n'en fini jamais,
car c'est n multiple de 2 qui permet de diviser en deux parts égales,
n multiple de 2 ne dit pas directement que c'est divisible par 2.
et hop une ligne de plus!

et donc les exigences d'écriture sont fonction du niveau des élèves.
on demandera plus de justification en primaire qu'en terminale sur une telle rédaction.
donc on accepte bien des sous-entendus,
dès lors qu'ils n'amènent pas à confusion.

par **paquito** » 02 Aoû 2014, 16:25

Quand j'ai préparé l'agrégation; le prof de spé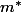

nous a prévenu: s'il voyait une "=>" dans une rédaction, il ne corrigeait même pas; c'était 0 pour la question!

Moi même, plus tard, je prévenais mes élèves, si je voyais une flèche, même brisée (flèche casio) dans une rédaction, je mettais 0 à a question.

Il y a assez de conjonctions de coordination pour faire une rédaction qui ait un sens. on ne va tout de même pas leur enseigner l'erreur de logique. l'"=>" n'a jamais permis d'affirmer qu'une proposition était vraie!

exception: pour définir une fonction sans la nommer et pour les limites.

Un devoir de mathématiques n'est pas un western!

par **beagle** » 02 Aoû 2014, 16:33

paquito a écrit:Quand j'ai préparé l'agrégation; le prof de spé nous a prévenu: s'il voyait une "=>" dans une rédaction, il ne corrigeait même pas; c'était 0 pour la question!

Moi même, plus tard, je prévenais mes élèves, si je voyais une flèche, même brisée (flèche casio) dans une rédaction, je mettais 0 à a question.

Il y a assez de conjonctions de coordination pour faire une rédaction qui ait un sens. on ne va tout de même pas leur enseigner l'erreur de logique. l'"=>" n'a jamais permis d'affirmer qu'une proposition était vraie!

exception: pour définir une fonction sans la nommer et pour les limites.

Un devoir de mathématiques n'est pas un western!

Je t'ai mis un exemple de problème.
j'y réponds
n multiple de 4 implique n multiple de 2
donc oui je peux mettre dans deux boites,
ce n'est pas du western,
le cas n non multiple de 4 n'a pas à ètre envisagé.

pour moi c'est de la psychorigidité

beaucoup de choses sont sous-entendues et si pas de confusion possibles,
je trouve cette attitude idiote.

par **zygomatique** » 02 Aoû 2014, 16:34

où l'on voit que bien parler français suffit amplement pour mener une démonstration à bien sans y incruster des symboles mathématiques ....

quant à Beagle je ne comprends pas ce qu'il raconte ....

par **beagle** » 02 Aoû 2014, 16:36

zygomatique a écrit:...
quant à Beagle je ne comprends pas ce qu'il raconte ....

Oui, c'est assez triste d'ailleurs.

par **paquito** » 02 Aoû 2014, 16:46

beagle a écrit:Prenons un exemple.
on distribue le mème nombre de bonbons à Julie,Manon, Kevin et Karim.
Peut-on ranger les bonbons dans deux boites contenant le mème nombre de bonbons.

n multiple de 4 implique n multiple de deux
donc oui je peux ranger les bonbons dans deux boites.

Vous considérez cela une non démonstration,
alors qu'il ne s'agit que de sous-entendus non écrits,
l'élève n'écrivant pas n est bien multiple de 4 puisque chacun des 4 personnages a le mème nombre de bonbons,
donc un langage qui n'énonce pas tout, un raccourci.

mais alors on n'en fini jamais,
car c'est n multiple de 2 qui permet de diviser en deux parts égales,
n multiple de 2 ne dit pas directement que c'est divisible par 2.
et hop une ligne de plus!

et donc les exigences d'écriture sont fonction du niveau des élèves.
on demandera plus de justification en primaire qu'en terminale sur une telle rédaction.
donc on accepte bien des sous-entendus,
dès lors qu'ils n'amènent pas à confusion.

L'énoncé entraîne que n soit multiple de 4, donc p est vraie; c'est comme si tu avais dit:" ils ont 40 bonbons" évidemment si p est forcément vraie, q sera vraie! si tu dis Julie, Manon,Kevin et Karin ont n bonbons, que devient la proposition" n est un multiple de 2"; elle ne vaut rien, strictement rien, ne sert à rien; elle peut être vraie comme fausse; donc tu prends un exemple où p est vraie d'office, donc q est vraie, mais n multiple de 4 =>p multiple de 2 est vraie avec n=9 et p=5; Si on te dit que c'est délicat!

par **paquito** » 02 Aoû 2014, 16:54

Quand un élève, et c'est courant, part de ABC rectangle pour aboutir à ABC rectangle, il na rien a démontrer, puisque si ABC est rectangle et bien il est rectangle.
C'est une confusion très courante entre p=>q et q=>p; ce qui prouve que"=>" n'a rien d'évident!

Question

Question

Qui est en ligne