Récurrence - Exo 9
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 10:45
par Okarin » 31 Juil 2014, 10:45
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 31 Juil 2014, 11:00
par MacManus » 31 Juil 2014, 11:00
Bonjour,
les coefficients binomiaux

sont des entiers naturels. Puisque f est à valeurs dans

, une telle suite
)
existe. Si une telle suite n'existait pas, tu aurais une somme finie d'entiers naturels et f serait à valeurs dans

C'est ce que je dirais, mais c'est peut-être pas très rigoureux...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 12:04
par zygomatique » 31 Juil 2014, 12:04
salut
en d'autres termes ::
pour toute fonction f : N --> Z il faut prouver qu'il existe une suite d'entiers relatifs
)
tel que ...
et il faut utiliser la récurrence je pense pour construire au fur et à mesure cette suite ...
ainsi tu as :
 = \sum_0^0 a_0 \binom 0 0 = a_0)
 = \sum_0^1 a_k \binom 1 k = a_0 + a_1 = f(0) + a_1)
donc
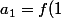 - f(0))
supposons qu'on a construit les n premiers termes de la suite .... et construisons le n+ 1-ième ...
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 31 Juil 2014, 12:51
par Sake » 31 Juil 2014, 12:51
Je proposerais de montrer que pour tout n et pour tout k plus petit que n, k parmi n est un entier (ce qui est, par définition, vrai).

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 12:57
par zygomatique » 31 Juil 2014, 12:57
Sake a écrit:Je proposerais de montrer que pour tout n et pour tout k plus petit que n, k parmi n est un entier (ce qui est, par définition, vrai).
je ne comprends pas ....
par contre pour la récurrence il suffit de connaître la relation entre C(n + 1, k) et C(n, k)
à chaque fois on a une équation du premier degré à une inconnue [/TEX]a_{n + 1}[TEX]
donc ça marche ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 31 Juil 2014, 13:00
par Sake » 31 Juil 2014, 13:00
zygomatique a écrit:je ne comprends pas ....
On veut que f soit à valeurs dans Z. Puisque (alpha_n) est une suite d'entiers relatifs, on a qu'à montrer que la combinaison des k parmi n est entière, cette propriété se transmettant - par linéarité de la sommation - à f(n).

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 13:02
par zygomatique » 31 Juil 2014, 13:02
Sake a écrit:On veut que f soit à valeurs dans Z. Puisque (alpha_n) est une suite d'entiers relatifs, on a qu'à montrer que la combinaison des k parmi n est entière, cette propriété se transmettant - par linéarité de la sommation - à f(n).
non on ne veut pas .... on sait que ....
ensuite ce n'est pas f qu'il faut construire à partir d'une suite c'est la suite qu'il faut construire à partir de f donnée ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 13:03
par Okarin » 31 Juil 2014, 13:03
Par exemple pour l'initialisation, est-ce que mon raisonnement doit ressembler à quelque chose comme ça :
PROPRIETE
P(n) :
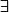
(
 \in \mathbb{N}^n)
tel que

p


,

(p) =
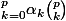
INITIALISATION
 = \sum_0^0 a_0 \binom 0 0 = a_0)
,
donc il existe un entier relatif de la suite 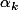
(ici
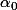
) et la propriété est bien vérifiée pour n = 0.
Comment vérifier que l'initialisation est bien vérifiée sinon ? Sur quoi s'appuyer ? C'est ça que j'ai du mal à comprendre.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 13:05
par zygomatique » 31 Juil 2014, 13:05
Okarin a écrit:Par exemple pour l'initialisation, est-ce que mon raisonnement doit ressembler à quelque chose comme ça :
PROPRIETE
P(n) :
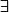
(
 \in \mathbb{N}^n)
tel que

p


,

(p) =
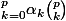
INITIALISATION
 = \sum_0^0 a_0 \binom 0 0 = a_0)
,
donc il existe un entier relatif de la suite 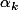
(ici
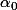
) et la propriété est bien vérifiée pour n = 0.
Comment vérifier que l'initialisation est bien vérifiée sinon ? Sur quoi s'appuyer ? C'est ça que j'ai du mal à comprendre.
non !!
supposons construits

, ...,

et donc
f(p) = ... pour 0 =< p =< n
il faut alors "calculer" f(n + 1) et déterminer
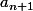
donc ce n'est pas

mais

...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 13:14
par Okarin » 31 Juil 2014, 13:14
zygomatique a écrit:non !!
supposons construits

, ...,

et donc
f(p) = ... pour 0 =< p =< n
il faut alors "calculer" f(n + 1) et déterminer
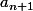
donc ce n'est pas

mais

...
Sans faire de récurrence alors ?
Comment faire l'initialisation sinon ? Je ne vois toujours pas la logique.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 31 Juil 2014, 13:44
par arnaud32 » 31 Juil 2014, 13:44
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 13:53
par Okarin » 31 Juil 2014, 13:53
arnaud32 a écrit: =\bigsum_{k=0}^{n+1} \alpha_k \binom{n+1}{k}=\alpha_{n+1}+\bigsum_{k=0}^{n} \alpha_k \binom{n+1}{k})
d'ou
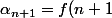-\bigsum_{k=0}^{n} \alpha_k \binom{n+1}{k})
et on bien

Comment peut-on conclure que

et non

par exemple ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 13:58
par zygomatique » 31 Juil 2014, 13:58
Okarin a écrit:Comment peut-on conclure que

et non

par exemple ?
parce que toute combinaison linéaire d'entiers à coefficients entiers est entière ...
la récurrence est encore plus simple que je ne le pensais ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 14:14
par Okarin » 31 Juil 2014, 14:14
Donc pour être sûr d'avoir compris, je dois modifier mon initialisation d'avant :
Okarin a écrit:PROPRIETE
P(n) :
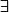
(
 \in \mathbb{N}^n)
tel que

p


,

(p) =
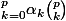
INITIALISATION
 = \sum_0^0 a_0 \binom 0 0 = a_0)
, donc il existe un entier relatif de la suite
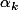
(ici
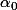
) et la propriété est bien vérifiée pour n = 0.
Comme ceci :
INITIALISATION
 = \sum_0^0 a_0 \binom 0 0 = a_0)
, et vu que par propriété (ci-dessus)

et que

, on a bien

et la propriété est bien vérifiée pour n = 0.
Ca me paraît trop subtil comme changement pour paraître juste... :hein:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Juil 2014, 14:58
par zygomatique » 31 Juil 2014, 14:58
Okarin a écrit:Donc pour être sûr d'avoir compris, je dois modifier mon initialisation d'avant :
Comme ceci :
INITIALISATION
 = \sum_0^0 a_0 \binom 0 0 = a_0)
, et vu que par propriété (ci-dessus)

et que

, on a bien

et la propriété est bien vérifiée pour n = 0.
Ca me paraît trop subtil comme changement pour paraître juste... :hein:
voir à 14h05 .....
le problème c'est la propriété P(n) ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Okarin
- Messages: 6
- Enregistré le: 31 Juil 2014, 10:01
-
 par Okarin » 31 Juil 2014, 15:15
par Okarin » 31 Juil 2014, 15:15
zygomatique a écrit:voir à 14h05 .....
le problème c'est la propriété P(n) ....
J'en profite alors pour reposer ma question de 14h14...
D'autre part, pouvez-vous svp m'expliquer en quoi ma propriété P(n) est fausse ?
Merci encore !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 31 Juil 2014, 15:40
par arnaud32 » 31 Juil 2014, 15:40
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 01 Aoû 2014, 00:24
par Razes » 01 Aoû 2014, 00:24
@Okarin
pour écrire

en
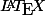
taper \mathbb{Z}
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
