Ensemble de définition d une fonction

[nour2013]

salut
au niveau du lycée
on utilise la terminologie ensemble de définition d une fonction et parfois domaine de définition
est ce qu il ya une différence car certains profs de maths utilisent l une et disent que l une des terminologie est fausse laquelle des deux et pourquoi

merci bien

[MacManus]

Bonjour,

Franchement ensemble/domaine de définition, c'est la même chose. Par contre, il ne faut pas confondre l'ensemble de départ d'une fonction avec son ensemble de définition...

[beagle]

salut
au niveau du lycée
on utilise la terminologie ensemble de définition d une fonction et parfois domaine de définition
est ce qu il ya une différence car certains profs de maths utilisent l une et disent que l une des terminologie est fausse laquelle des deux et pourquoi

merci bien

Je n'en sais rien, mais j'ai un peu peur que le problème soit plus psychologique et en rapport avec le degré de psychorigidité du prof.

j'en sais rien mais le mieux est d'utiliser les termes du prof, donc le laisser parler le premier!!!

et en cas de force majeur je trouve assez drole de dire
soit Df l'ensemble de défintion de ...
(sachant que ensemble commence par E et domaine commence par D, hi,hi,hi...

En attendant les puristes...

[Emolga]

Comme dit, l'ensemble de définition : est l'ensemble des éléments de qui possèdent une image dans

est encore le domaine de définition de : ce n'est pas l'ensemble sauf si'Il arrive que les deux soient égaux : la fonction est alors une application bien définie partout dans .

[MacManus]

En fait je dirais qu'un ensemble de définition peut-être soit:
- un sous-ensemble de l'ensemble de départ de la fonction f (dans ce cas on peut dire ensemble=domaine)
- égal à l'ensemble de départ de la fonction f

et un domaine est toujours:
- un sous-ensemble de l'ensemble de départ de la fonction f.

Biensûr, quand on parle d'ensemble/domaine de définition, cela induit une correspondance (fonction) qui pour tout x de l'ensemble/domaine de définition, associe au plus une image notée f(x).

Encore un histoire de patates !

[nour2013]

salut

donc on utilise domaine de définition lorsque f est une application( définition et différence avec fonction) et ensemble de définition lorsque f est une fonction
qu on f est définie sur un intervalle de IR ou bien sur une réunion d intervalle
est ce qu il ya une relation avec la terminologie utiliser
si possible de m expliquer d avantage

[MacManus]

Oui moi je le vois comme ça en tout cas.

[zygomatique]

salut

une fonction est une opération qui s'éxécute sur des objets

une fonction numérique s'exécute sur les nombres
la fonction dérivation s'exécute sur des fonctions


prenons l'ensemble des nombres R et les fonctions numériques réelles

on y rencontre la fonction , , 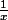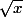qui peuvent s'exécuter sur tous ou certains nombres ...

DEF : l'ensemble de définition d'une fonction f est l'ensemble des réels x tels que f(x) existe ...

et dans tous les cas le domaine de définition est R

le codomaine d'une fonction numérique réelles est alors aussi R ... et qui n'est pas toujours identique à l'image de f ....

[nour2013]

[quote="zygomatique"]salut

quelle est la différence donc entre ensemble de définition et domaine de définition
est ce que
l une des terminologie est spécifique pour les applications et l autre pour les fonctions
ou bien lorsque une fonction est définie sur un seul intervalle de IR et pas sur la réunion de plusieurs intervalles

toujours pas très claire

[Sylviel]

nour : pour mémoire il est explicitement interdit de mettre "urgent" dans le titre...

[zygomatique]

il y a simplement une différence quand on dit :

domaine de f

domaine de définition de f = ensemble de définition de f

...

[beagle]

Je ne saisi pas bien les nuances*,
alors pourquoi ne pas renverser le problème:
donner des exemples de phrases qui heurtent ou peuvent heurter un prof ...

*:"l'ensemble de définition d'une fonction f est l'ensemble des réels x tels que f(x) existe ...

et dans tous les cas le domaine de définition est R"

[zygomatique]

Je ne saisi pas bien les nuances*,
alors pourquoi ne pas renverser le problème:
donner des exemples de phrases qui heurtent ou peuvent heurter un prof ...

*:"l'ensemble de définition d'une fonction f est l'ensemble des réels x tels que f(x) existe ...

et dans tous les cas le domaine de définition est R"

oui bien vu .... :bad:

et dans tous les cas le domaine est R ....