Notation theta
18 messages
- Page 1 sur 1
Notation theta
Bonjour,
Je bloque sur un problème qui ne me parait pas si difficile que ça. (ce qui m'énerve encore plus!)
Il s'agit d'un problème d'algorithmique consistant à montrer que an²+bn+c=;)(n²), avec a>0.
Rappel : Pour une fonction g(n), on note ;)(g(n)) l'ensemble de fonctions suivant :
;)(g(n))= { f(n) : il existe des constantes positives c1, c2 et n0 telles que 0<=c1*g(n)<=f(n)<=c2g(n) pour tout n>=n0 }
Il est écrit sur mon livre "On prend c1=a/4, c2=7a/4 et n0=2*max((|b|/a), Sqrt(|c|/a))."
Et je n'arrive pas à obtenir n0 à partir de c1 et c2. J'ai essayé de résoudre simplement les deux inégalités séparément, cela consiste à résoudre un polynôme de second degré, mais mes solutions sont bien plus compliquées que 2*|b|/a ou 2*Sqrt(|c|/a). Je pense que je n'attaque pas le problème sous le bon angle, pouvez-vous éclairer ma lanterne s'il vous plait ?
Merci d'avance !
Je bloque sur un problème qui ne me parait pas si difficile que ça. (ce qui m'énerve encore plus!)
Il s'agit d'un problème d'algorithmique consistant à montrer que an²+bn+c=;)(n²), avec a>0.
Rappel : Pour une fonction g(n), on note ;)(g(n)) l'ensemble de fonctions suivant :
;)(g(n))= { f(n) : il existe des constantes positives c1, c2 et n0 telles que 0<=c1*g(n)<=f(n)<=c2g(n) pour tout n>=n0 }
Il est écrit sur mon livre "On prend c1=a/4, c2=7a/4 et n0=2*max((|b|/a), Sqrt(|c|/a))."
Et je n'arrive pas à obtenir n0 à partir de c1 et c2. J'ai essayé de résoudre simplement les deux inégalités séparément, cela consiste à résoudre un polynôme de second degré, mais mes solutions sont bien plus compliquées que 2*|b|/a ou 2*Sqrt(|c|/a). Je pense que je n'attaque pas le problème sous le bon angle, pouvez-vous éclairer ma lanterne s'il vous plait ?
Merci d'avance !
zygomatique a écrit:salut
posons
donc on cherche u et v et un rang à partir duquel
et on te dit que u = a/4 et v = 7a/4 conviennent
ben si il faut effectivement résoudre les inéquations :
à toi maintenant de bien mener les calculs ...
Mince ... c'est pourtant ce que j'essayais de faire ! Je vais me repencher sur ça de façon plus attentive !
EDIT : Prenons la première inégalité.
Le discriminant vaut donc b²-3ac.
1er cas :
2e cas :
3e cas :
Encore merci !
car a > 0
on fait la même chose pour l'autre inégalité ... et puisqu'on a la réponse on essaie dans les deux pour voir ce qu'on obtient ....
REM : il n'est peut-être même pas besoin de transformer : on essaie les deux valeurs directement dans les deux inégalités et on regarde .....
de toute façon le discriminant risque fort d'être négatif ... et c'est pourquoi on s'impose un rang à partir duquel c'est vrai ...
donc on remplace simplement n par |b|/a et par sqrt (|c|/a) dans chaque inégalité et on regarde ...
si effectivement on n'avait pas les résultats ça serait plus compliqué ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Excuse moi, mais je ne saisis pas bien où nous mène la transformation de cette inégalité. Sauf pour voir que les valeurs fonctionnent ? Est-ce bien ça ?
Ce que j'aimerais savoir, c'est comment trouver n0 à partir du choix de c1 et c2 : "faire semblant" de ne pas connaitre n0 en quelques sortes ! (ce qu'a fait l'auteur du livre à priori)
Pourquoi ?
Merci beaucoup de ton aide.
Ce que j'aimerais savoir, c'est comment trouver n0 à partir du choix de c1 et c2 : "faire semblant" de ne pas connaitre n0 en quelques sortes ! (ce qu'a fait l'auteur du livre à priori)
de toute façon le discriminant risque fort d'être négatif ...
Pourquoi ?
Merci beaucoup de ton aide.
Zanshi a écrit:Excuse moi, mais je ne saisis pas bien où nous mène la transformation de cette inégalité. Sauf pour voir que les valeurs fonctionnent ? Est-ce bien ça ?
Ce que j'aimerais savoir, c'est comment trouver n0 à partir du choix de c1 et c2 : "faire semblant" de ne pas connaitre n0 en quelques sortes ! (ce qu'a fait l'auteur du livre à priori)
Pourquoi ?
Merci beaucoup de ton aide.
tu as deux fonctions
soit pour tout x > 0 :: f(x) > g(x) et le discriminant est strictement négatif et on ne s'emmerde pas à chercher un rang pour lequel c'est vrai ....
soit justement f(x) > g(x) à partir d'un certain rang et donc c'est que le discriminant est positif !!!
mais le calcul du discriminant ne nous intéresse pas c'est le rang ....
on cherche donc un réel u > 0 tel que si x > u alors on est sur que f(x) > g(x) ....
ensuite pour u il suffit de le prendre supérieure à la racine positive éventuelle du trinôme f(x) - g(x)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Merci pour cet éclaircissement zygomatique.
Peut-on calculer ce rang ?
Bonjour deltab,
Leur limite est + l'infini (car a>0), on en déduit que pour n suffisamment grand, f(n) est comprise entre an²/4 et 7an²/4 (que an²/4 croît moins vite que f(n) et inversement pour 7an²/4). Le tout est de calculer ce n suffisamment grand.
Tout à fait, je le comprends parfaitement ça, en revanche je n'arrive pas à calculer n_0, ce qui devrait être possible une fois C_1 et C_2 choisis arbitrairement. (mais respectant tout de même la condition que tu as soulevé)
Merci à vous deux !
EDIT :
Pour u il suffit de le prendre supérieure à la racine positive éventuelle du trinôme, donc le calcul du discriminant nous intéresse, non ? Sans discriminant, pas de racine ?
Ta dernière phrase est particulièrement intéressante, c'est ce que je "craignais". L'auteur aurait-il fait en sorte de prendre un u ayant une forme sympathique supérieure à la racine ? (Méthode de Newton par exemple?)
soit justement f(x) > g(x) à partir d'un certain rang et donc c'est que le discriminant est positif !!!
Peut-on calculer ce rang ?
Bonjour.
Calcules la limite quand n \to + \infty de f(n)-\dfrac{an^2}{4} et celle de \dfrac{7an^2}{4}-f(n). Que peut-on en déduire par définition de la limite
Bonjour deltab,
Leur limite est + l'infini (car a>0), on en déduit que pour n suffisamment grand, f(n) est comprise entre an²/4 et 7an²/4 (que an²/4 croît moins vite que f(n) et inversement pour 7an²/4). Le tout est de calculer ce n suffisamment grand.
Remarque: Toutes valeurs de C_1 et C_2 vérifiant 0<C_1<a <C_2 vont donner la même résultat avec n_0 dépendant de C_1 et C_2.
On a un résultat analogue pour f(n) un polynôme de degré n\ge 1 de coefficient dominant a>0
Tout à fait, je le comprends parfaitement ça, en revanche je n'arrive pas à calculer n_0, ce qui devrait être possible une fois C_1 et C_2 choisis arbitrairement. (mais respectant tout de même la condition que tu as soulevé)
Merci à vous deux !
EDIT :
mais le calcul du discriminant ne nous intéresse pas c'est le rang ....
on cherche donc un réel u > 0 tel que si x > u alors on est sur que f(x) > g(x) ....
ensuite pour u il suffit de le prendre supérieure à la racine positive éventuelle du trinôme f(x) - g(x)
Pour u il suffit de le prendre supérieure à la racine positive éventuelle du trinôme, donc le calcul du discriminant nous intéresse, non ? Sans discriminant, pas de racine ?
Ta dernière phrase est particulièrement intéressante, c'est ce que je "craignais". L'auteur aurait-il fait en sorte de prendre un u ayant une forme sympathique supérieure à la racine ? (Méthode de Newton par exemple?)
Bonjour
@
Quand je t'ai dit de calculer les limites et toutes les ddeux valaient , j'ai ajouté:
, j'ai ajouté:
Soit une fonction telle que
telle que =+\infty) alors par définition
alors par définition
 telle que pour tout
telle que pour tout >A)
Pour A=1, on obtient telle que pour tout
telle que pour tout >1>0)
On aura pour-\dfrac{ax^2}{{4}) , il existe
, il existe  tel que
tel que -\dfrac{ax^2}{4}>0) et pour
et pour ) , il existe
, il existe  tel que
tel que >0) .
.
Il suffit de prendre pour que
pour que <\dfrac{7ax^2}{4})
A toi de modifier la démonstration si et
et  sont dans
sont dans 
@
Quand je t'ai dit de calculer les limites et toutes les ddeux valaient
Que peut-on en déduire par définition de la limite (avec A=1)
Soit une fonction
Pour A=1, on obtient
On aura pour
Il suffit de prendre
A toi de modifier la démonstration si
Ah mince, je n'avais pas fait attention au A=1
Cela revient à ce que j'ai dit, non ? f(x) encadré par ax²/4 et 7ax²/4 ? Je ne vois toujours pas en quoi cela fait avancer le problème. Je veux "simplement" avoir n_0 par le calcul. Toutes les considérations à côté, je pense les avoir comprises. J'ai bien compris pourquoi on avait un n_0 = au maximum de deux valeurs (qui sont x_1 et x_2 dans ton texte). Je ne remets pas en doute (et je sais prouver) son existence, là n'est pas mon problème.
A moins que je ne vois vraiment pas où vous voulez en venir, et dans ce cas : mea culpa.
Cela revient à ce que j'ai dit, non ? f(x) encadré par ax²/4 et 7ax²/4 ? Je ne vois toujours pas en quoi cela fait avancer le problème. Je veux "simplement" avoir n_0 par le calcul. Toutes les considérations à côté, je pense les avoir comprises. J'ai bien compris pourquoi on avait un n_0 = au maximum de deux valeurs (qui sont x_1 et x_2 dans ton texte). Je ne remets pas en doute (et je sais prouver) son existence, là n'est pas mon problème.
A moins que je ne vois vraiment pas où vous voulez en venir, et dans ce cas : mea culpa.
Bonsoir
La méthode que j'ai proposé donne l'existence de C_1, C_2, exemple C_1=a/2, C_2=3a/2 et la définition de la limite donne l'existence de . Comme je ne connais pas les signes de
. Comme je ne connais pas les signes de  et
et  , j'ai pris
, j'ai pris  , prendre
, prendre  ne permet d"affirmer que
ne permet d"affirmer que 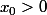
Pour avoir une valeur de en fonction de
en fonction de  et
et  (donc en fonction de
(donc en fonction de  ), il faudra résoudre les 2 inéquations et montrer que celles-ci admettent un ensemble de solutions sous la forme d'un intervalle non borné {u,+\infty[ u étant exprimé en fonction de a.
), il faudra résoudre les 2 inéquations et montrer que celles-ci admettent un ensemble de solutions sous la forme d'un intervalle non borné {u,+\infty[ u étant exprimé en fonction de a.
Ceci est faisable si est un polynôme de degré 1 ou 2 , fastidieux et long si
est un polynôme de degré 1 ou 2 , fastidieux et long si  est un polynôme de degré 3 ou 4 , voire impossible si
est un polynôme de degré 3 ou 4 , voire impossible si  est un polynôme de degré 5 ou plus.
est un polynôme de degré 5 ou plus.
Zanshi a écrit:Ah mince, je n'avais pas fait attention au A=1
Cela revient à ce que j'ai dit, non ? f(x) encadré par ax²/4 et 7ax²/4 ? Je ne vois toujours pas en quoi cela fait avancer le problème. Je veux "simplement" avoir n_0 par le calcul. Toutes les considérations à côté, je pense les avoir comprises. J'ai bien compris pourquoi on avait un n_0 = au maximum de deux valeurs (qui sont x_1 et x_2 dans ton texte). Je ne remets pas en doute (et je sais prouver) son existence, là n'est pas mon problème.
A moins que je ne vois vraiment pas où vous voulez en venir, et dans ce cas : mea culpa.
La méthode que j'ai proposé donne l'existence de C_1, C_2, exemple C_1=a/2, C_2=3a/2 et la définition de la limite donne l'existence de
Pour avoir une valeur de
Ceci est faisable si
Ok, merci à vous deux.
Je le savais déjà ça, mais merci pour la formalisation. En ce qui concerne les signes de x_1, et x_2, le problème ne se pose pas dans mon cas -mais c'est parce que je me place dans le cadre de complexité algorithmique, ce sont des maths très appliquées, x_1 et x_2 sont forcément positifs-.
Tout le problème est là, faute d'avoir trouvé une réponse satisfaisante, je pense abandonner mes recherches pour le moment. Quoi qu'il en soit, merci beaucoup à vous deux !
La méthode que j'ai proposé donne l'existence de C_1, C_2, exemple C_1=a/2, C_2=3a/2 et la définition de la limite donne l'existence de x_0. Comme je ne connais pas les signes de x_1 et x_2, j'ai pris x_0= \max\lbrace1,x_1,x_2\rbrace, prendre x_0 =\max\lbrace x_1,x_2\rbrace ne permet d"affirmer que x_0>0
Je le savais déjà ça, mais merci pour la formalisation. En ce qui concerne les signes de x_1, et x_2, le problème ne se pose pas dans mon cas -mais c'est parce que je me place dans le cadre de complexité algorithmique, ce sont des maths très appliquées, x_1 et x_2 sont forcément positifs-.
Pour avoir une valeur de x_0 en fonction de C_1 et C_2 (donc en fonction de a ), il faudra résoudre les 2 inéquations et montrer que celles-ci admettent un ensemble de solutions sous la forme d'un intervalle non borné {u,+\infty[ u étant exprimé en fonction de a.
Tout le problème est là, faute d'avoir trouvé une réponse satisfaisante, je pense abandonner mes recherches pour le moment. Quoi qu'il en soit, merci beaucoup à vous deux !
Bonsoir.
La définition de)}) ne fait qu'intervenir que l'existence des 3 constantes
ne fait qu'intervenir que l'existence des 3 constantes  ,
,  et
et  .
.
Ici et C_2 sont explicitement donnés en fonction de
et C_2 sont explicitement donnés en fonction de  .
.
Le calcul de en fonction de
en fonction de  n'est pas demandé et si on le fait, ça va conduire pour chacune des deux inéquations à des discutions en fonction du signe du discriminant
n'est pas demandé et si on le fait, ça va conduire pour chacune des deux inéquations à des discutions en fonction du signe du discriminant  . Dans le cas où les deux discriminants sont négatifs, on peut prendre
. Dans le cas où les deux discriminants sont négatifs, on peut prendre 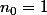
La définition de
Ici
Le calcul de
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
