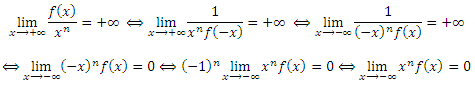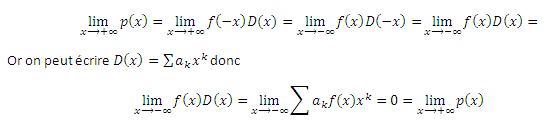Cet été, pour éviter de nous rouiller, notre professeur de mathématiques nous a donné une fiche d'exercices plus ou moins difficiles à essayer. Je les ai presque tous terminés, mais en voilà un qui me pose beaucoup de problèmes! Peut-être trouverez-vous des idées? Voici l'énoncé!

Voilà déjà ce que j'ai fait. Pour tout l'exercice, j'ai considéré qu'il ne fallait pas déterminer une telle fonction, mais je me suis parfois inspiré de a^x pour mener certains raisonnements.
1)
- Pour cette question, quelque chose de très étrange, en dérivant, j'obtiens g'(y) = f'(x+y)f(-y) - f(x+y)f(-y), ce qui, puisque f(X)=f'(X) fait 0, et non pas f(x)... Et pourtant, j'ai bien l'impression que g(y) est une fonction constante. A partir de là, je me dis que si g(y) est constant. Alors, on peut remarquer que g(y) = g(0) = f(x).
- Ca, c'est bon.
- De même.
- Là, je bloque... J'ai l'impression que "ça se voit", mais je ne sais pas comment le justifier...
- Puisque f(x) > 0, f'(x) > 0 et donc f(x) est croissante.
2)
- Là, c'est une question où j'utilise une méthode un peu étrange, je pense. Je me suis dit que x + 1 = f'(0)(x-0) + f(0) = f(0)(x-0+1), c'est-à-dire que c'est l'équation de la tangente au point d'abscisse 0. En partant de ça, puisque je sais que f(x) est croissante, je me suis dit que la courbe de f(x) était nécessairement au-dessus de cette tangente (encore du "ça se voit"^^), d'où le fait que f(x) > x + 1. Mais je suis bien conscient que mon argumentation ici est assez douteuse.
- J'utilise l'idée précédente en remplaçant x par x/2 ce qui me permet d'obtenir f(x/2)² > x²/4 (+ 1 + x). Ensuite, je me dis que f(x/2)² = f(x/2)f(x/2) = f(x) d'après la première question. Produit en croix puisque x > 0 qui amène à f(x)/x > x/4.
- f(x)/x est supérieure à une fonction affine, qui tend vers l'infini. D'où le résultat.
- Alors là... Je ne sais plus quoi dire, d'autant que ce sont des résultats qui ne me paraissent pas intuitifs du tout!
3) C'est la question non guidée, à priori... Mais évidemment, je pense qu'il faut se servir des résultats précédents, notamment avec le x^nf(x)... Par ailleurs, en dérivant la fonction qu'ils proposent d'étudier, je trouve f(-x)P(x)... Je me suis certainement trompé.
Voilà, je trouve que l'exercice est difficile... Si vous avez une idée, ce serait vraiment formidable de me donner une piste pour une question laissée en suspens. Au fait, je ne suis qu'en Première S et ne dispose que des outils que nous avons vu pour le résoudre...
Merci pour votre lecture et peut-être pour votre réponse! Très bonne soirée!