Voici l'exercice : Montrer (sans récurrence) que
Polynome divisibilité
17 messages
- Page 1 sur 1
Polynome divisibilité
Bonjour je fais un exercice sur les polynôme mais je ne comprends pas comment on s'y prend pour le faire
Voici l'exercice : Montrer (sans récurrence) que divise
divise ^{2n}-1)
 divise (
divise (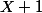^n -nX-1) et que
et que
^2) divise
divise X^n +1)
Voici l'exercice : Montrer (sans récurrence) que
Bonjour
Si un polynôme) est divisible par
est divisible par ^p) ,
,  entier >0, alors
entier >0, alors =0) et ......
et ......
PS: revois l'énoncé de cette partie: divise
divise ^2n) -1
-1
George150 a écrit:Bonjour je fais un exercice sur les polynôme mais je ne comprends pas comment on s'y prend pour le faire
Voici l'exercice : Montrer (sans récurrence) quedivise
-1
divise (
et que
divise
Si un polynôme
PS: revois l'énoncé de cette partie:
x-a divise P ? Donc on doit chercher les racines de a pour prouver la divisilbilité ?
a c'est un scalaire, ce que tu dis n'as pas de sens.
Eventuellement tu peux dire "chercher les racines du polynome x-a"
Concernant ton exo, la def de divisibilité des polynomes c'est genre quand tu les divises tu obtiens un autre polynome.
Si tu décomposes chacun de tes polynomes en facteurs, genre (x-a)(x-a)(x-b) etc, (ici a racine double), alors il faut que dans la liste des racines du polynome divisé, toutes les racines du polynome diviseur y soient comprises.
(pour que les facteurs se simplifient)
En l'occurrence, tu peux:
factoriser X^2+X, genre (X(X+1)) et regarder que ses racines, 0 et -1 soient bien racines de l'autre polynome. Idem P(0)=0, P(-1)=0
la vie est une fête 
si a est racine double du polynome P,
alors a est racine de P'.
Si a est racine double de P,
Si t'écris P(x)=(x-a)^alpha*Q(x), (donc avec alpha>1) avec Q qui n'a pas a pour racine, alors si tu dérives
P'(x)=alpha(x-a)^(alpha -1)Q(x)+Q'(x)(x-a)^alpha = (x-a)^(alpha-1)(alpha Q(x)+Q'(x)(x-a)^alpha
et on voit bien que a est bien racine de P'(x)
De manière plus générale si a est une racine d'ordre n, alors le polynome dérivée n+1 fois admet également cette racine.
alors a est racine de P'.
Si a est racine double de P,
Si t'écris P(x)=(x-a)^alpha*Q(x), (donc avec alpha>1) avec Q qui n'a pas a pour racine, alors si tu dérives
P'(x)=alpha(x-a)^(alpha -1)Q(x)+Q'(x)(x-a)^alpha = (x-a)^(alpha-1)(alpha Q(x)+Q'(x)(x-a)^alpha
et on voit bien que a est bien racine de P'(x)
De manière plus générale si a est une racine d'ordre n, alors le polynome dérivée n+1 fois admet également cette racine.
la vie est une fête 
fatal_error a écrit:si a est racine double du polynome P,
alors a est racine de P'.
Si a est racine double de P,
Si t'écris P(x)=(x-a)^alpha*Q(x), (donc avec alpha>1) avec Q qui n'a pas a pour racine, alors si tu dérives
P'(x)=alpha(x-a)^(alpha -1)Q(x)+Q'(x)(x-a)^alpha = (x-a)^(alpha-1)(alpha Q(x)+Q'(x)(x-a)^alpha
et on voit bien que a est bien racine de P'(x)
De manière plus générale si a est une racine d'ordre n, alors le polynome dérivée n+1 fois admet également cette racine.
Ah merci beaucoup ! Donc pour la dernière phrase c'est qu'on doit dérivé le polynôme n fois et montré que chaque dérivé vaut admet la même racine pour montrer que c'est un divisible ?
Bonsoir
Ce n'est pas plutôt: On montre que P(0) = 0 et il faut faire la même chose pour P'(0) = 0 où=(X-1)^n-nX-1) .
.
Il est évident que 0 est une racine double de=X^2) . Si
. Si  divise
divise  alors
alors 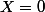 est au moins une racine double de
est au moins une racine double de  et on doit alors avoir
et on doit alors avoir =0) et
et =0) , ceci se démontre rapidement en calculant P(0) et P'(0).
, ceci se démontre rapidement en calculant P(0) et P'(0).
George150 a écrit:Je viens de recevoir la correction, la voici pour la 2ème:
Notons Q(x) =divise (
. On montre que Q(0) = 0 et il faut faire la même chose pour Q'(0) = 0 Quelqu'un peut m'expliquer pourquoi on dérive ?
Ce n'est pas plutôt: On montre que P(0) = 0 et il faut faire la même chose pour P'(0) = 0 où
Il est évident que 0 est une racine double de
@fatal_error
C'est plutôt:
De manière plus générale si est une racine d'ordre
est une racine d'ordre ) d'un polynôme
d'un polynôme) , alors ses dérivées
, alors ses dérivées }(X)) jusqu'à l'ordre
jusqu'à l'ordre  admettent également
admettent également  pour racine mais
pour racine mais  n'est pas racine de
n'est pas racine de }(X)) .
.
De manière plus générale si a est une racine d'ordre n, alors le polynôme dérivée n+1 fois admet également cette racine.
C'est plutôt:
De manière plus générale si
Bonjour
NON Dans le cas traité=X^2) c'est pourquoi X=0.
c'est pourquoi X=0.
Pour=(X-1)^2) divise
divise =nX^{n+1}-(n+1)X^n+1) , la racine à considérer est
, la racine à considérer est 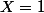 , racine double de
, racine double de ) . On calcule P(1) et P'(1).
. On calcule P(1) et P'(1).
PS: As-tu suivi un cours où l'on parle des différents résultats utilisés.
George150 a écrit:Ah okey merci ! Donc il faut toujours que X vaut 0 et que P(0) = 0 pour que ça marche ? (ainsi que ses dérivées jusqu'à n-1)
NON Dans le cas traité
Pour
PS: As-tu suivi un cours où l'on parle des différents résultats utilisés.
1) Nous avons ) et
et =(X+1)^{2n}-1)
Si divise
divise ) alors
alors  divise
divise ) et
et  divise
divise ) . Donc les racines de
. Donc les racines de  sont aussi racines de
sont aussi racines de ) .
.
Nous avons=(0+1)^{2n}-1=1^{2n}-1=0) et
et =(-2+1)^{2n}-1=(-1)^{2n}-1=1-1=0)
Donc effectivement divise
divise ) .
.
2) Nous avons et
et =(X+1)^{n}-nX-1)
 a une racine double qui est
a une racine double qui est 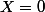 . Donc pour que
. Donc pour que  divise
divise ) il faut que X divise
il faut que X divise ) et
et  divise
divise ) . avec :
. avec : =n(X+1)^{n-1}-n)
Nous avons=(0+1)^{n}-n0-1=1-1=0) et
et =n(0+1)^{n-1}-n=n-n=0)
Donc effectivement divise
divise ) .
.
3) Même chose qu'en 2)^2) a une racine double qui est
a une racine double qui est 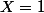 .
.
=nX^{n+1}-(n+1)X^{n}+1) et
et =n(n+1)X^{n}-n(n+1)X^{n+1}=n(n+1)(X^{n}-X^{n+1}))
=n1^{n+1}-(n+1)1^{n}+1 =0) et
et =n(n+1)(1^{n}-1^{n+1})=0)
Donc^2) divise
divise ) .
.
Si
Nous avons
Donc effectivement
2) Nous avons
Nous avons
Donc effectivement
3) Même chose qu'en 2)
Donc
prérequis : le binôme de Newton .... (BN)
1/
^{2n} - 1 = ((x + 1)^n - 1)((x + 1)^n + 1))
BN nous dit que x divise le premier facteur ...
^{2n} - 1 = (x + 2 - 1)^{2n} - 1)
Bn nous dit que x + 2 divise le polynome
or x et x + 2 sont premiers entre eux donc x(x + 2) divise ce polynôme ....
2/
BN nous dit immédiatement que divise
divise ^n - nx - 1)
3/
x^n + 1 = nx^n(x - 1) - (x^n - 1) = (x - 1)(nx^n - \sum_0^{n - 1} \ x^k) = (x - 1)\sum_0^{n - 1}(x^n - x^k) = (x - 1)\sum_0^{n - 1}x^k(x^{n - k} - 1))
or x - 1 divise chaque terme de la somme donc^2) divise le polynôme
divise le polynôme
:zen:
merci à MacManus pour l'erreur d'énoncé ...
1/
BN nous dit que x divise le premier facteur ...
Bn nous dit que x + 2 divise le polynome
or x et x + 2 sont premiers entre eux donc x(x + 2) divise ce polynôme ....
2/
BN nous dit immédiatement que
3/
or x - 1 divise chaque terme de la somme donc
:zen:
merci à MacManus pour l'erreur d'énoncé ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
