Aide intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bouti1008
- Messages: 2
- Enregistré le: 15 Juil 2014, 10:05
-
 par bouti1008 » 15 Juil 2014, 10:15
par bouti1008 » 15 Juil 2014, 10:15
Bonjour,
je suis bloquée dans la résolution d'une intégrale.
Voici mon problème :
Calculer l'intégrale de 0 à ln(2) de sqrt(exp(x)-1) en fonction de x
J'ai posé t=exp(x). Et donc j'obtiens
l'intégrale de 1 à 2 de (sqrt(t-1))/t en fonction de t
A ce stade je ne sais pas comment continuer.
Pouvez-vous m'aider?
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 15 Juil 2014, 11:04
par MacManus » 15 Juil 2014, 11:04
Bonjour,
Tu peux faire le changement de variable suivant:
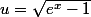

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Juil 2014, 11:41
par zygomatique » 15 Juil 2014, 11:41
salut
il me semble que
 = e^x - 1)
puis une (ou deux) IPP convenables peut suffire ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MacManus
- Membre Irrationnel
- Messages: 1365
- Enregistré le: 28 Avr 2008, 14:41
-
 par MacManus » 15 Juil 2014, 11:46
par MacManus » 15 Juil 2014, 11:46
Peut-être je n'ai pas essayé. En tout cas en posant u=sqrt(exp(x)-1) le calcul ne nécessite aucune IPP.
-
bouti1008
- Messages: 2
- Enregistré le: 15 Juil 2014, 10:05
-
 par bouti1008 » 15 Juil 2014, 12:11
par bouti1008 » 15 Juil 2014, 12:11
Super merci beaucoup :)
Je l'ai fait en posant u=sqrt(exp(x)-1) et effectivement ca va tout seul ;)
merci
 par techno20aout » 15 Juil 2014, 15:46
par techno20aout » 15 Juil 2014, 15:46
généralement la résolution des intégrales se base sur deux cas:
1) changement de variable
2) intégrales par parties
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 16 Juil 2014, 00:50
par deltab » 16 Juil 2014, 00:50
Bonjour
zygomatique a écrit:salut
il me semble que
 = e^x - 1)
puis une (ou deux) IPP convenables peut suffire ....
Intuition erronée concernant les IPP, un autre changement nous ramène à comme si on avait posé au début
 = \sqrt{e^x - 1})
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
