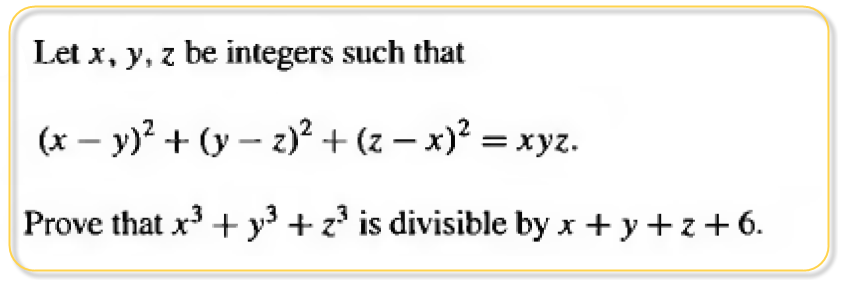Prove that
35 messages
- Page 1 sur 2 - 1, 2
Prove that
Prove that x^9999+ x^8888+ x^7777+
.+ x^2222+ x^1111+ 1 is divisible by x^9+ x^8+ x^7+
.+ x^2+ x+ 1
Hello there,
This is a French speaking forum. It'd be great if you could at least have the decency to say hello and to translate your questions so that you could reach out to more people.
Thanks. (For I will have to lock the thread if no translation is further provided)
This is a French speaking forum. It'd be great if you could at least have the decency to say hello and to translate your questions so that you could reach out to more people.
Thanks. (For I will have to lock the thread if no translation is further provided)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Est-ce que tu as déjà testé des entiers ?
Par exemple , x = 2 , y=1, z=3
(x - y)² + (y - z)² + (z - x)² = (1)² + (-2)² + (1)² = 1 + 4 +1 = 6
xyz= 2*3*1 = 6 donc c'est l'égalité est vérifiée
Sinon pour le reste , tu dois revoir les identités remarquables , et les trucs avec les règles de fractions .
Un truc à savoir :
(x+y+z)^3 = (x^3+y^3+z^3)+3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2)+6xyz
x^3+y^3+z^3 = -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 6xyz
= -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 12
x^3+y^3+z^3 = -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 6xyz
= -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 12
= -3(-6) - 12
= 18 - 12
= 6
Par exemple , x = 2 , y=1, z=3
(x - y)² + (y - z)² + (z - x)² = (1)² + (-2)² + (1)² = 1 + 4 +1 = 6
xyz= 2*3*1 = 6 donc c'est l'égalité est vérifiée
Sinon pour le reste , tu dois revoir les identités remarquables , et les trucs avec les règles de fractions .
Un truc à savoir :
(x+y+z)^3 = (x^3+y^3+z^3)+3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2)+6xyz
x^3+y^3+z^3 = -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 6xyz
= -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 12
x^3+y^3+z^3 = -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 6xyz
= -3(x^2y+x^2z+xy^2+y^2z+xz^2+yz^2) - 12
= -3(-6) - 12
= 18 - 12
= 6
Lostounet a écrit:Hello there,
This is a French speaking forum. It'd be great if you could at least have the decency to say hello and to translate your questions so that you could reach out to more people.
Thanks. (For I will have to lock the thread if no translation is further provided)
Comment tu parles un anglais trop formel lostounet
lulubibi28 a écrit:Oui , mais c'est vrai que le titre du topic est un peu rude ^^
En tout cas , "integers" veut dire un entier .
@brhum.moh Sinon , pour la divisibilité , là dans cet exo , il doit y avoir une astuce ...
salut
il y a une formule
x³+y³+y³=(x+y+z)(x²+y²+z²-xy-xz-yz)+3xyz
on développe l'égalité de l'hypothèse et on remplace.
il y juste à montrer que x, y et z ne sont pas tous les trois impairs et c'est simple à faire.
J'ai pensé à poser x+y+z=sigma1
xy+yz+xz=sigma2 et xyz=sigma3
A partir de (x-y)²+(y-z)²+(z-x)²=xyz on obtient 2*(sigma1²-2*sigma2)=2*sigma2+sigma3
Et à partir de x^3+y^3+z^3 je développe et j'ai que c'est égal à sigma1(sigma1²-2*sigma2)
Ca avance pas à grand chose mais j'ai pas le temps de trop pousser mes recherches et de toute façon les fonctions symétriques servent plutôt lorsqu'on cherche des propriétés utiles avec les racines d'un polynôme bien précis. Ici c'était pour simplifier les calculs.
xy+yz+xz=sigma2 et xyz=sigma3
A partir de (x-y)²+(y-z)²+(z-x)²=xyz on obtient 2*(sigma1²-2*sigma2)=2*sigma2+sigma3
Et à partir de x^3+y^3+z^3 je développe et j'ai que c'est égal à sigma1(sigma1²-2*sigma2)
Ca avance pas à grand chose mais j'ai pas le temps de trop pousser mes recherches et de toute façon les fonctions symétriques servent plutôt lorsqu'on cherche des propriétés utiles avec les racines d'un polynôme bien précis. Ici c'était pour simplifier les calculs.
Salut,
Un truc bien utile pour ce genre de casse-tête, c'est les Identités de Newton donnant le lien entre les sommes de Newton et les polynômes symétriques élémentaires :
Si
alors
donc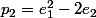 et
et 
en dévelopant, l'hypothèse dit que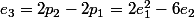 .
.
Donc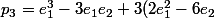=e_1^3+6e_1^2-3e_1e_2-18e_2=(e_1+6)(e_1^2-3e_2))
est bien divisible par
Un truc bien utile pour ce genre de casse-tête, c'est les Identités de Newton donnant le lien entre les sommes de Newton et les polynômes symétriques élémentaires :
Si
alors
donc
en dévelopant, l'hypothèse dit que
Donc
est bien divisible par
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
35 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :