Theoreme de deux chemins(fct a plusieurs variables)

[Bazvindous]

salut a tous, l'application de deux chemins pour un repere (x,y) ce fais en rapprochons le pts (x,y) soit par une droite(y=x, y=mx etc) ou un courbe(..).
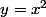
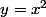
Et pour un plan (x,y,z) comment faire?? est ce par deux droite(y=x et z=x etc) ou courbe( et z=...) simultanements qu'on rapproche le pts (x,y,z)??
merci a vous.

[Ben314]

Salut,
Je comprend pas trop la question : c'est quoi ton "théorème des deux chemins" et ça veut dire quoi "l'application de deux chemins" ?


P.S. : j'apprécie pas trop qu'on mette les mêmes questions sur deux les forums...
http://www.ilemaths.net/forum-sujet-607924.html
ça donne un peu l'impression que tu t'en fout que des mecs perdent du temps à t'expliquer un truc... qu'on t'a déjà expliqué ailleurs...

[Bazvindous]

salut,

c'est quoi ton "théorème des deux chemins" et ça veut dire quoi "l'application de deux chemins" ?

C'est pas un theoreme a moi, sinon je ne demanderais pas de l'aide,bref.
LA LIMITE DES FONCTIONS A PLUSIEURS VARIABLES.
Pour demontrer qu'ils n'existent pas, on passe par ce theoreme(deux chemins).
Il consiste a faire rapprocher le repere sur l'un des axes(abs ou ord) ou/et par l'origine.

ça donne un peu l'impression que tu t'en fout que des mecs perdent du temps à t'expliquer un truc... qu'on t'a déjà expliqué ailleurs...

Quelle idee Ben314!!!!, les explications ne sont pas les mm(au contraire c'est avec appreciation que je les lisent).Le plus souvent ca vient du fait qu'on prends trop de temps et parfois mm ignorer certaine question sur des forums qu'on a l'idee d'y poster aillieur.
merci a vous.

[zygomatique]

salut

un chemin dans l'espace ou dans le plan ... il n'y a aucune différence quand on pense à des courbes paramétrées .... et non pas qu'à des courbes représentant des fonctions

ainsi

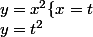
de même dans l'espace il suffit de considérer un chemin

x = f(t)
y = g(t)
z = h(t)

avec les limites nécessaires pour faire ce que l'on veut ....

évidemment après correction ...

bien sur si z = F(x, y) on ne prend que les deux premières ....

:hum:

[deltab]

Bonjour,

salut,

C'est pas un theoreme a moi, sinon je ne demanderais pas de l'aide,bref.
LA LIMITE DES FONCTIONS A PLUSIEURS VARIABLES.
Pour demontrer qu'ils n'existent pas, on passe par ce theoreme(deux chemins).
Il consiste a faire rapprocher le repere sur l'un des axes(abs ou ord) ou/et par l'origine.

Quelle idee Ben314!!!!, les explications ne sont pas les mm(au contraire c'est avec appreciation que je les lisent).Le plus souvent ca vient du fait qu'on prends trop de temps et parfois mm ignorer certaine question sur des forums qu'on a l'idee d'y poster aillieur.
merci a vous.

Les deux posts ont été faits avec un intervalle d'une heure entre les deux, le 1er de plus à minuit.
Tu parlais d'un théorème ( à énoncer de préférence) concernant la non existence de la limite d'une fonction à 2 variables en un point donné que tu voulais généraliser pour une fonction à 3 variables. La réponse est OUI sauf qu'il faut prendre deux courbes distinctes, le système d'équations définit 2 surfaces donc au plus une courbe.

[Bazvindous]

Aaa ok, Merci a vous.a t'il un moyen de cocher resolut??

[Sourire_banane]

Tu modifies ton premier post.

[Bazvindous]

Tu modifies ton premier post.....

Vous voulez dire qoui???

[deltab]

Bonsoir,

Aaa ok, Merci a vous.a t'il un moyen de cocher resolut??

Tu viens de le faire!

[deltab]

Bonsoir,

Tu modifies ton premier post.

Si les messages qui ont suivi ne citent pas ceux auxquels ils ont répondu, cela risque de dénaturer certaines réponses et même les rendre incompréhensibles. Je suis d'avis à garder le message original et y ajouter à la suite les modifications.

[Sourire_banane]

Bonsoir,


Si les messages qui ont suivi ne citent pas ceux auxquels ils ont répondu, cela risque de dénaturer certaines réponses et même les rendre incompréhensibles. Je suis d'avis à garder le message original et y ajouter à la suite les modifications.

Non mais c'est pour modifier le titre et rajouter "résolu"...