Voilà mon petit exercice : Je voulais savoir pour qu'elle valeur de
où m est un entier naturel .
Je sais que cette intègrale converge pour
Merci beaucoup d'avance.
Convergence d'integrale
3 messages
- Page 1 sur 1
convergence d'integrale
par geo » 17 Juin 2014, 12:30
Bonjour Tout le monde !!
Voilà mon petit exercice : Je voulais savoir pour qu'elle valeur de
cette intégrale converge :
^{(\alpha-1)(m-1)}}{(U_{1}...U_{m})^{\alpha}}dU_{1}...dU_{m})
où m est un entier naturel .
Je sais que cette intègrale converge pour
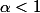
pour le problème en zéro mais comment faire pour le problème à l'infini .
Merci beaucoup d'avance.
Voilà mon petit exercice : Je voulais savoir pour qu'elle valeur de
où m est un entier naturel .
Je sais que cette intègrale converge pour
Merci beaucoup d'avance.
par mr_pyer » 17 Juin 2014, 14:46
Salut !
J'ai l'impression que cette intégrale ne converge jamais.
Exemple avec m=2 après être passé en coordonnées polaires :
+r\sin(t))^{\alpha-1}}{r^{2\alpha}\cos^\alpha(t)\sin^\alpha(t)}rdrdt.)
En
, l'intégrande est en 
.
En dimension
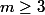
on a du 
qui apparaît et le même phénomène se produit.
J'ai l'impression que cette intégrale ne converge jamais.
Exemple avec m=2 après être passé en coordonnées polaires :
En
En dimension
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :