Problème d'intégrale vectorielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
h.borie
- Messages: 6
- Enregistré le: 22 Mai 2014, 14:38
-
 par h.borie » 11 Juin 2014, 15:21
par h.borie » 11 Juin 2014, 15:21
Bonjour je suis confronté à un problème d'électromagnétisme couplé à un soucis de discrétisation par éléments finis.
Après un calcul je réussi à récupérer certaines données sur ce problème.
Sur une surface modéliser par éléments finis, j'ai :
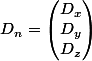
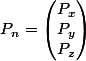
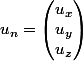
Avec :
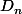
: champs des déplacéments électrique (induction électrique) au noeud

: Position initiale du noeud

: déplacement du noeud
A partir de là je veux calculer la charge électrique nodale tel que :

or est-ce que
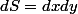
avec
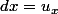
et
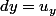
Mais je ne sais pas comment interpréter cela ni comment le calculer car je n'ai jamais fait d'intégration vectorielle surfacique sur un problème élément finis?
Merci d'avance,
Cordialement.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 12 Juin 2014, 05:25
par Cliffe » 12 Juin 2014, 05:25
Dans quel repère sont donnés les vecteurs.
Toutes les composantes sont constantes ?
-
h.borie
- Messages: 6
- Enregistré le: 22 Mai 2014, 14:38
-
 par h.borie » 12 Juin 2014, 10:00
par h.borie » 12 Juin 2014, 10:00
Toutes les composantes des vecteurs sont des scalaires.
La surface sur laquelle on intègre est un disque de normale

.
Les vecteurs ont pour repère (0,
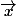
,
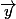
,

).
Ce sont des constantes car récupérerce sont des valeurs à un instant donné pour un noeud du maillage.
Quelques choses pourrait peut-être servir. J'ai trouvé quelques part :
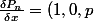)
avec

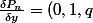)
avec
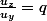
on pose
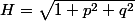
H est la norme du produit vectoriel

alors
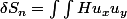
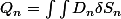
Cela vous parle-t-il?
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 12 Juin 2014, 15:32
par Cliffe » 12 Juin 2014, 15:32
Si c'est constant alors
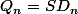
.
-
h.borie
- Messages: 6
- Enregistré le: 22 Mai 2014, 14:38
-
 par h.borie » 13 Juin 2014, 08:58
par h.borie » 13 Juin 2014, 08:58
Mais malheureusement ce n'est pas un problème continu mais discret. J'ai une surface maillée et je récupère les vecteurs sur chaque noeuds de la surface. Je ne sais donc pas comment faire pour effectuer l'intégrale surfacique pour chaque noeud.
Cela peut-il être vraiment aussi simple que
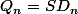
?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 13 Juin 2014, 09:13
par fatal_error » 13 Juin 2014, 09:13
hello,
sur 1D, pour deux points A(a,b), B(c,d), on peut choisir comme valeur le point au milieu C((a+b)/2, (c+d)/2), et considérer l'aire ((c+d)/2] * (c-a), pis faire pareil pour tous les points.
pour 2D, je ferais pareil.
tu prends 4 points adjacents, ca te donne un quadrilatère dont tu calcules la surface, et tu prends le point moyen.
et tu calcules le volume associé.
Pis tu sommes tous les volumes.
en tout cas c'est ce que l'intuition souffle!
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
