Deux équations de tangente pas évidente :/

[mistiratop]

Bonjour,

Pour finir l'année en beauté,notre professeur de math nous a donné un dernier exercice a faire à la maison.Cette exercice de fin d'année n'est pas évident du tout et je demande votre aide afin de le résoudre.

Voici l'énoncé :
'' T(1;2) - A(4;5)

C cercle de centre T et de rayon 2

1) A appartient-t-il à C ?
2) Déterminer une équation des tangentes à C passant par A ''

Pour la 1),j'ai écris :

''Le cercle C de centre T(1;2) et de rayon 2 a pour équation cartésienne : (x-1)^2 + (y-2)^2 = 4

Remplacons x par xA et y par yA :

(4-1)^2 + (5-2)^2 = 2 x (3^2) = 18 or 18 différent de 4,donc A n'appartient pas à C''

Pour la 2) j'ai tenté quelquechose :

''A n'appartient pas au cercle C,il y a donc deux tangentes à C qui passe par A.

Ces tangentes sont des droites,elles ont alors pour équation y = ax + c
or A appartient à ces droites,donc yA=axA + c 5 = 4a + c c = 5-4a

Appelons d et d' les deux tangentes.

d et d' ont une équation du type y = ax + c ax - y + c = 0 ax - y + 5-4a = 0

On calcule desormais la distance D du point T a une de ces tangentes

d(T,d) = d(T,d') = D = 2 or par définition, D = lax - y + 5 -4al/Va^2 + 1 car b est le coefficient de y soit -1''

Ensuite je fais un produit en croix,je résout l'équation et je tombe sur deux équations invraisemblables

en voici une : '' y = (-9+V56/-5)x + 5 - 4*((-9+V56/-5). (V = racine de)

Merci de bien vouloir m'aider et de corriger mes erreurs si je me suis trompé (ceux dont je suis quasiment sur face à cette équation x)

Cordialement , Mistiratop.

[paquito]

Soit M un des 2 points de contact; tu as 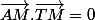, soit x²-5x+4+y²-7x+14=0; ensuite, tu as x²-2x+y²-4y+1=0; tu en déduit par différence:
-3x-3y=-13, d'où y=-x+13/3 (c'est l'équation de la droite passant par les 2 points de contacts M1 et M2 que l'on obtient en construisant le cercle de diamètre[T;A]); en reportant, tu obtiens
, ce qui te donneras les 2 valeurs de x (j'ai refais plus sérieusement les calculs!). en s'appliquant, on trouve: dont les solutions permettent de trouver les coordonnée de M1 et M2; ça donne:
, et


Evidemment, obtenir des résultats aussi laids est normalement inquiétant et on cherche où on a pu faire une erreur! Mais tout est juste, j'ai vérifié sur géogébra; c'est perturbant bien sûr!

Ensuite, est un vecteur normal à la tangente (T1) qui admet comme éqation:

; il reste a remplacer x et y par 4 et 5 et on obtient c =. Je t'épargne la suite; le but était seulement de te montrer une autre méthode et te rappeler une construction géométrique des tangentes.

[chan79]

salut
les équations cherchées sont de la forme y=mx+p soit y=mx+5-4m sachant que si x=4, y doit être égal à 5.
On remplace y dans l'équation du cercle (x-1)²+(y-2)²=4
on obtient une équation en x dont le discriminant doit être nul
ce qui amène à résoudre 5m²-18m+5=0
ou
et il suffit de remplacer m pour obtenir les équations des tangentes
l'une est

ce qui correspond à ton résultat