Fonction Sinus et Cosinus
19 messages
- Page 1 sur 1
Fonction Sinus et Cosinus
Bonjour,
j'ai lu dans un corrigé la chose suivante :
cos(x+pi/6)=(cos(x).cos(pi/6)-sin(x).sin(pi/6))
Je ne comprends pas vraiment pourquoi on peut dire cela ? Est ce que quelqu'un pourrait m'expliquer.
Merci beaucoup d'avance !
j'ai lu dans un corrigé la chose suivante :
cos(x+pi/6)=(cos(x).cos(pi/6)-sin(x).sin(pi/6))
Je ne comprends pas vraiment pourquoi on peut dire cela ? Est ce que quelqu'un pourrait m'expliquer.
Merci beaucoup d'avance !
bsr
en passant par les exponentielles complexes
exp(ia)=cos(a) + isin(a)
exp(ib)=cos(b) + isin(b)
le produit des 2 exp=exp i(a+b) = [cos(a) + isin(a)][cos(b) + isin(b)]= cos(a+b) + i sin(a+b)
=cos(a+b) =partie réelle du produit
= cos(a).cos(b) + i² sin(a).sin(b)
or le complexe i²=-1
d'ou cos(a+b)= cos(a).cos(b) - sin(a).sin(b)
mais il existe d'autre demo
en passant par les exponentielles complexes
exp(ia)=cos(a) + isin(a)
exp(ib)=cos(b) + isin(b)
le produit des 2 exp=exp i(a+b) = [cos(a) + isin(a)][cos(b) + isin(b)]= cos(a+b) + i sin(a+b)
=cos(a+b) =partie réelle du produit
= cos(a).cos(b) + i² sin(a).sin(b)
or le complexe i²=-1
d'ou cos(a+b)= cos(a).cos(b) - sin(a).sin(b)
mais il existe d'autre demo
Salut !
Plaçons-nous dans le repère orthonormal direct) .
.
Soient et
et 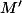 deux points du cercle trigo tels
deux points du cercle trigo tels = a) et
et = b) .
.
En projetant le vecteur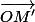 sur la droite
sur la droite ) (cela revient à calculer
(cela revient à calculer  ), on a
), on a =\vec{OM'}\cdot\vec{OM}) .
.
Plaçons-nous dans le repère orthonormal direct
Soient
En projetant le vecteur
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
AllanPoe a écrit:Je cherchais aussi a savoir comment résoudre cette inéquation :
cos(x+pi/6)<0
Résoudre dans un intervalle en particulier ou sur
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
AllanPoe a écrit:Je ne comprends pas le rapport avec sin
Je ne comprends pas ce que tu veux dire...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Plaçons-nous dans le repère orthonormal direct.
Soientet
deux points du cercle trigo tels
et
.
En projetant le vecteursur la droite
(cela revient à calculer
), on a
.
Quelles sont les coordonnées des vecteurs
Déduis-en alors le produit scalaire
Ensuite, connaissant
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Quelles sont les coordonnées des vecteurset
?
Déduis-en alors le produit scalaire(c'est-à-dire
).
Ensuite, connaissant, tu peux trouver
en remplaçant
par
dans
.
Ahhh okok je connais ça ça me dis quelque chose merci !
Et pour l'inéquation
une petite piste pour la manière de résoudre
AllanPoe a écrit:Et pour l'inéquation
une petite piste pour la manière de résoudre
Y a-t-il un intervalle particulier pour la résoudre ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
