Question : Trigonalisation

[psp]

Bonjour,

Je souhaite avoir des conseils sur comment trigonaliser une matrice.

Je dis tout d'abord que son polynôme caractéristique étant scindé, je peux trigonaliser.
Je détermine les sous-espaces caractéristiques associés aux valeurs propres.
Maintenant les problèmes se posent pour moi.
1/ Est-ce la famille des sous-espaces caractéristiques qui forme la matrice de passage ?
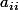
2/ Ma matrice trigonale, je sais que ses valeurs sont les valeurs propres de la matrice initiale, mais comment déterminer les autres valeurs ? Je n'ai pas pu aller plus loin que déterminer les sous-espaces propres associés aux valeurs propres, les mettre dans la matrice de passage (ça marche car les s.e.p sont inclus dans les s.e.c), et du coup les vecteurs (de la matrice trigonale) correspondant aux sous espaces propres sont de la forme (0,0,..,a(ii),0,0,0,..,0), mais je ne peux pas faire ça pour toutes les valeurs propres sinon cela voudrait dire que la matrice est diagonalisable ce qui n'est pas le cas

Pouvez vous m'aider s'il vous plait ?
Merci

[psp]

J'ai une autre méthode que je trouve fastidieuse, je prends la famille des sous espaces propres, je la complète pour former la matrice de passage, je l'inverse et applique la formule
Mais j'aimerai directement trouver les valeurs de la matrice trigonale sans avoir a inverser la matrice de passage, je sais que c'est possible mais je n'y arrive pas

[elvis77]

une fois que tu as les sous espaces propres, il ne te manque plus qu'à compléter les * dans la matrice, par exemple :

tu as et
tu peux ainsi trouver *.
Ainsi de suite.
Cordialement.