Bonjour,
voici mon problème :
je dispose de N vecteurs dans un plan 2D (N grand et connu)
la norme de ces vecteurs suit une loi normale (moyenne M ; ecart-type E) connue
leurs directions est aléatoire
soit V le vecteur résultant de la somme de ces N vecteurs.
je voudrais savoir si j'ai assez d'informations pour connaître l'espérance et l'ecart-type de la norme de V ? et comment je pourrais les calculer ? merci
Question de statistique
12 messages
- Page 1 sur 1
stocke a écrit:oui la loi de répartition des directions est uniforme sur [0;2*pi]
et oui chaque vecteur est indépendant
Bonjour,
prendre une loi normale pour la norme est assez étrange puisqu'elle peut prendre des valeurs négatives (à moins de considérer pour le calcul qu'une norme négative revient à modifier de Pi l'orientation du vecteur).
Mais bon quelque soit les lois, si tu as tes N vecteurs de norme (Vi) et de direction (ai), tu peux les projeter sur les axes : xi = Vi cos(ai) et yi = Vi sin(ai)
alors la résultante a pour composante X = somme( Vi cos(ai) ) et Y = somme( Vi sin(ai) )
et puis la norme sera racine(X²+Y²). Calculer son espérance et sa variance de facon analytique sera probablement très délicat analytiquement vu la racine. Si le besoin est purement numérique un Monte-Carlo fera ça très bien.
En revanche, pour les composantes X et Y, l'espérance est 0 c'est logique, et pour la norme au carré X²+Y² il doit y avoir moyen de faire quelque chose analytique : l'espérance donnera sauf erreur quelque chose comme N*E(V²), V étant la loi de la norme, quant à la variance ça doit se trouver aussi. On retombe bien sur le déplacement "moyen" proportionnel à la racine du nombre de pas, résultat bien connu pour une marche aléatoire 2d dont cette question en est un exemple.
Damien
zygomatique a écrit:salut
on approxime bien la loi binomiale par une loi normale ... je ne vois pas en quoi est-ce gênant d'approximer la distributions des normes par une loi normale ...
Tout dépend ce qu'on en fait, mais la possibilité d'avoir des normes négatives, au-delà d'être aberrant, peut provoquer quelques artefacts non désirables selon les calculs effectués par la suite, mais en l'occurence ce n'est pas le cas en considérant les projections sur les axes.
Quant à la somme de complexes, l'espérance fait 0 mais ce n'est pas du tout la question posée...
Damien
Bonjour,
les normes négatives ne sont pas vraiment un problème, puisque j'utilise une loi normale avec une moyenne élevée et un écart-type faible (les normes négatives deviennent à ce moment très rares).
Par curiosité, j'ai appliqué Monte Carlo pour N=100, moyenne=10 et ecart-type=0.3
J'obtiens pour le module de la somme des vecteurs un histogramme qui ressemble à une gaussienne déformée (plus aplatie pour les valeurs élevées que pour les valeurs faibles) dont l'espérance est non nulle.
Pouvez-vous me dire comment je doit procéder pour obtenir analytiquement cette espérance en fonction de N, de la moyenne et de l'ecart-type ? (Idéalement le mieux pour mon problème serait d'obtenir un intervalle dans lequel mon module final ait 90% de s'y retrouver)
les normes négatives ne sont pas vraiment un problème, puisque j'utilise une loi normale avec une moyenne élevée et un écart-type faible (les normes négatives deviennent à ce moment très rares).
Par curiosité, j'ai appliqué Monte Carlo pour N=100, moyenne=10 et ecart-type=0.3
J'obtiens pour le module de la somme des vecteurs un histogramme qui ressemble à une gaussienne déformée (plus aplatie pour les valeurs élevées que pour les valeurs faibles) dont l'espérance est non nulle.
Pouvez-vous me dire comment je doit procéder pour obtenir analytiquement cette espérance en fonction de N, de la moyenne et de l'ecart-type ? (Idéalement le mieux pour mon problème serait d'obtenir un intervalle dans lequel mon module final ait 90% de s'y retrouver)
Bonjour,
Analytiquement on trouve très facilement l'espérance de la norme au carré du vecteur somme comme déjà écrit :
En reprenant les mêmes notations on a :
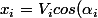, y_i = V_isin(\alpha_i))
Alors le vecteur somme a pour composantes :
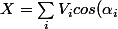, Y = \sum_i V_isin(\alpha_i))
et la norme au carré du vecteur est donc
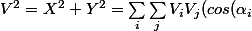cos(\alpha_j)+sin(\alpha_i)sin(\alpha_j)))
Qui est in fine la variable aléatoire que l'on souhaite étudier.
On peut la réécrire en isolant les termes i=j ce qui donne :
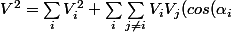cos(\alpha_j)+sin(\alpha_i)sin(\alpha_j)))
car cos²+sin²=1
Partant de là, l'espérance tombe direct puisque les variables) sont indépendantes et d'espérance nulle (l'intégrale du cosinus sur 0,2Pi est 0), idem pour les
sont indépendantes et d'espérance nulle (l'intégrale du cosinus sur 0,2Pi est 0), idem pour les ) , du coup on a tout simplement :
, du coup on a tout simplement :
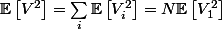 car les Vi sont de même loi.
car les Vi sont de même loi.
La variance de V² est elle aussi calculable avec un peu plus d'effort car on tombera sur des [TEX] \mathbb{E}\left[cos^2(\alpha_i)\right] qui valent 1/2.
Quant à obtenir l'intervalle de confiance 90% analytiquement, cela me paraît plus délicat, et si les gaussiennes initiales sont assez resserrées, une approximation bateau avec les deux premiers moments que l'on vient d'obtenir pourra peut être suffire.
Damien
Analytiquement on trouve très facilement l'espérance de la norme au carré du vecteur somme comme déjà écrit :
En reprenant les mêmes notations on a :
Alors le vecteur somme a pour composantes :
et la norme au carré du vecteur est donc
Qui est in fine la variable aléatoire que l'on souhaite étudier.
On peut la réécrire en isolant les termes i=j ce qui donne :
car cos²+sin²=1
Partant de là, l'espérance tombe direct puisque les variables
La variance de V² est elle aussi calculable avec un peu plus d'effort car on tombera sur des [TEX] \mathbb{E}\left[cos^2(\alpha_i)\right] qui valent 1/2.
Quant à obtenir l'intervalle de confiance 90% analytiquement, cela me paraît plus délicat, et si les gaussiennes initiales sont assez resserrées, une approximation bateau avec les deux premiers moments que l'on vient d'obtenir pourra peut être suffire.
Damien
DamX a écrit:Bonjour,
Analytiquement on trouve très facilement l'espérance de la norme au carré du vecteur somme comme déjà écrit :
En reprenant les mêmes notations on a :
Alors le vecteur somme a pour composantes :
et la norme au carré du vecteur est donc
Qui est in fine la variable aléatoire que l'on souhaite étudier.
On peut la réécrire en isolant les termes i=j ce qui donne :
car cos²+sin²=1
Partant de là, l'espérance tombe direct puisque les variablessont indépendantes et d'espérance nulle (l'intégrale du cosinus sur 0,2Pi est 0), idem pour les
, du coup on a tout simplement :
car les Vi sont de même loi.
La variance de V² est elle aussi calculable avec un peu plus d'effort car on tombera sur des [TEX] \mathbb{E}\left[cos^2(\alpha_i)\right] qui valent 1/2.
Quant à obtenir l'intervalle de confiance 90% analytiquement, cela me paraît plus délicat, et si les gaussiennes initiales sont assez resserrées, une approximation bateau avec les deux premiers moments que l'on vient d'obtenir pourra peut être suffire.
Damien
Merci beaucoup pour votre aide, je vais voir si j'arrive à obtenir l'intervalle de confiance à partir de l'espérance et la variance
stocke a écrit:Merci beaucoup pour votre aide, je vais voir si j'arrive à obtenir l'intervalle de confiance à partir de l'espérance et la variance
EDIT : en googlant vite fait, je viens de trouver ce papier :
http://courses.biology.utah.edu/goldenberg/biol3820/lectMaterial/lect11/lecture11.pdf
qui exhibe explicitement la distribution du rayon d'une marche aléatoire 2d (c'est à dire de la norme de ton vecteur somme), en haut de la page 6, qui peut donc servir pour le calcul de l'intervalle. J'ai lu rapidement, cela s'applique peut-être uniquement à une longueur fixe à chaque pas, à voir donc si ça doit être adapté.
Damien
DamX a écrit:EDIT : en googlant vite fait, je viens de trouver ce papier :
http://courses.biology.utah.edu/goldenberg/biol3820/lectMaterial/lect11/lecture11.pdf
qui exhibe explicitement la distribution du rayon d'une marche aléatoire 2d (c'est à dire de la norme de ton vecteur somme), en haut de la page 6, qui peut donc servir pour le calcul de l'intervalle. J'ai lu rapidement, cela s'applique peut-être uniquement à une longueur fixe à chaque pas, à voir donc si ça doit être adapté.
Damien
en effet il s'agit exactement du problème que je cherche à résoudre. Merci pour l'info :zen:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
