je suis bloquée à ces deux questions :
f un endomorphisme de base
5. Vérifier que
10.Soient
Déterminer explicitement
je pense qu'il faut utiliser ceci mais je n'y arrive pas.
si vous pouviez m'aider svp
Matrice
3 messages
- Page 1 sur 1
matrice
par encre bleu » 25 Mai 2014, 15:57
Bonjour,
je suis bloquée à ces deux questions :
f un endomorphisme de base
 \mapsto (-x+3y-2z,-x+3y-2z,-x+y))
5. Vérifier que \in Im(f))
10.Soient
 \in {(R^N)^3} avec {u_0}=1, {v_0}=-1,{w_0}=0 et \\<br />{u_{n+1}}=-{u_n}+3 {v_n}-2 {w_n}\\<br />{v_{n+1}}=-{u_n}+3 {v_n}-2 {w_n}\\<br />{w_{n+1}}=-{u_n}+{v_n} \\)
Déterminer explicitement
en fonction de n\
je pense qu'il faut utiliser ceci mais je n'y arrive pas.
=\begin{pmatrix}0&1&0\\<br />0&0&0\\<br />0&0&2\\<br />\end{pmatrix})
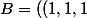, (0,1,1), (1,1,0)))
=\begin{pmatrix}0&0&0\\<br />0&0&0\\<br />0&2^n&0\\<br />\end{pmatrix})
si vous pouviez m'aider svp
je suis bloquée à ces deux questions :
f un endomorphisme de base
5. Vérifier que
10.Soient
Déterminer explicitement
je pense qu'il faut utiliser ceci mais je n'y arrive pas.
si vous pouviez m'aider svp
par Julien8 » 25 Mai 2014, 17:23
Pour la question 5 il suffit de poser le système correspondant et de faire du pivot de gauss ensuite.
par encre bleu » 25 Mai 2014, 17:55
Julien8 a écrit:Pour la question 5 il suffit de poser le système correspondant et de faire du pivot de gauss ensuite.
Désolée mais je ne vois pas, j'en ai déjà fait un pour la suite de la question
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :