Sous groupe

par **adamNIDO** » 23 Mai 2014, 10:19

Bonjour tout le monde,

Etant donnée

un groupe abélien et

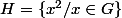
Est ce que

est sous-groupe de

? justifier votre réponse ?

En effet,

Dire que H est un sous-groupe de G si et seuelement si :

(i)

(ii) si

alors

(iii) si

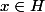
, alors

pour le point ii) soient

alors

ca l'aire que je peux pas vérifier ces conditions donc je peux dire que H n'est pas sous groupe de G

je suis bloqué la

par **Maxmau** » 23 Mai 2014, 10:48

adamNIDO a écrit:Bonjour tout le monde,

Etant donnée un groupe abélien et

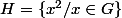
Est ce que est sous-groupe de ? justifier votre réponse ?

En effet,

Dire que H est un sous-groupe de G si et seuelement si :

(i)
(ii) si alors
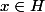
(iii) si , alors

pour le point ii) soient alors
ca l'aire que je peux pas vérifier ces conditions donc je peux dire que H n'est pas sous groupe de G

je suis bloqué la

Bj
G est abélien

par **adamNIDO** » 23 Mai 2014, 11:15

Maxmau a écrit:Bj
G est abélien

oui G abélien

par **Monsieur23** » 23 Mai 2014, 11:37

Aloha,

Tu prends x et y dans H : tu peux donc les écrire x = a^2 et y = b^2. Donc

par **bentaarito** » 23 Mai 2014, 13:25

adamNIDO a écrit:oui G abélien

Maxmau ne posait pas une question, mais t'as donné l'ultime point clé pour ton problème

G étant abélien, tu peux voir x²y² comme xyxy=(xy)²
(+ utilise l indication de Monsieur23 )

par **adamNIDO** » 23 Mai 2014, 14:35

bentaarito a écrit:Maxmau ne posait pas une question, mais t'as donné l'ultime point clé pour ton problème

G étant abélien, tu peux voir x²y² comme xyxy=(xy)²
(+ utilise l indication de Monsieur23 )

Merci beaucoup oui je vois

Sous groupe

sous groupe

Qui est en ligne