DM produit scalaire

[Bones3018]

Bonsoir, j'ai un DM à faire et je ne comprends pas du tout l'exercice.

On donne //vecteurU// = //vecteurV// = 1
Calculer vecteurU²-vecteurV² de deux façons. En déduire que (vecteurU + vecteurV) est perpendiculaire à (vecteurU - vecteurV)

Merci

[Ericovitchi]

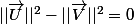
C'est pas bien compliqué, tu sais donc que d'une part et puis si tu appliques a²-b² (vectoriellement) et tu en déduis que ça vaut aussi et tu conclus.

[Bones3018]

Mais je dois trouver deux manières différentes d'arriver au résultat, je ne trouve pas la 2ème

[chan79]

Mais je dois trouver deux manières différentes d'arriver au résultat, je ne trouve pas la 2ème

salut
Comme te l'a dit Ericovitchi, d'une part c'est 0 et d'autre part, c'est

[Bones3018]

Je ne sais pas comment faire pour prouver qu'ils sont perpendiculaires

[Ericovitchi]

Si leur produit scalaire est nul, c'est qu'ils sont perpendiculaires.