Sommes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 10 Mai 2014, 13:38
par Gonra » 10 Mai 2014, 13:38
bonjour
je souhaite calculer la sommes des k(k-1) pour k allant de 2 à n sans passer par k^2-k ( car on me demande d'en déduire k² ensuite )
la somme vaut = 2 + 6 + 12 + 20 + 30 + 42 ....
pour passer de 2 de à 6 on ajoute 4 et de 6 à 12 on ajoute 6 puis 8 puis 10 etc
j'en déduit une suite :
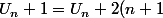)
avec
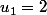
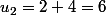
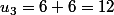
ça l'air de marcher mais je n'arrive pas à trouver l'expression de Un en fonction de n pour ensuite trouver la somme k(k-1)
on m'a aussi parler d'une polynôme qu'il fallait dériver qui donne directement la somme
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 10 Mai 2014, 13:53
par Manny06 » 10 Mai 2014, 13:53
Gonra a écrit:bonjour
je souhaite calculer la sommes des k(k-1) pour k allant de 2 à n sans passer par k^2-k ( car on me demande d'en déduire k² ensuite )
la somme vaut = 2 + 6 + 12 + 20 + 30 + 42 ....
pour passer de 2 de à 6 on ajoute 4 et de 6 à 12 on ajoute 6 puis 8 puis 10 etc
j'en déduit une suite :
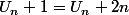
avec
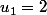
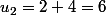
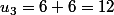
ça l'air de marcher mais je n'arrive pas à trouver l'expression de Un en fonction de n pour ensuite trouver la somme k(k-1)
on m'a aussi parler d'une polynôme qu'il fallait dériver qui donne directement la somme
peut -être en calculant la dérivée seconde de 1+x+x²+......+x^n
que tu peux calculer directement

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Mai 2014, 13:57
par zygomatique » 10 Mai 2014, 13:57
salut
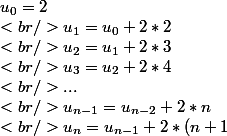)
et on ajoute membre à membre
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 10 Mai 2014, 14:33
par Manny06 » 10 Mai 2014, 14:33
Gonra a écrit:bonjour
je souhaite calculer la sommes des k(k-1) pour k allant de 2 à n sans passer par k^2-k ( car on me demande d'en déduire k² ensuite )
la somme vaut = 2 + 6 + 12 + 20 + 30 + 42 ....
pour passer de 2 de à 6 on ajoute 4 et de 6 à 12 on ajoute 6 puis 8 puis 10 etc
j'en déduit une suite :
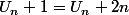
avec
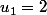
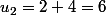
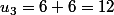
ça l'air de marcher mais je n'arrive pas à trouver l'expression de Un en fonction de n pour ensuite trouver la somme k(k-1)
on m'a aussi parler d'une polynôme qu'il fallait dériver qui donne directement la somme
si Un+1= Un+2n avec U1=2
U2=U1+2*1=2+2=4 ne serait ce pas plutôt Un+1=Un+2(n+1) ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Mai 2014, 15:33
par chan79 » 10 Mai 2014, 15:33
ça doit marcher par récurrence
2*1+3*2=3*2(1/3+1)=(2*3*4)/3
2*1+3*2+4*3=(2*3*4)/3+(4*3)=4*3(2/3+1)=(3*4*5)/3
tu peux essayer de montrer par récurrence que 2*1+3*2+4*3+ ... +n(n-1)=(n-1)n(n+1)/3
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 10 Mai 2014, 15:56
par nodjim » 10 Mai 2014, 15:56
Pour trouver la valeur approchée, c'est un bon réflexe de chercher l'intégrale....
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 10 Mai 2014, 17:32
par Gonra » 10 Mai 2014, 17:32
Merci pour votre aide je l'ai trouvé avec la récurrence finalement
je me suis rendu compte que la suite que j'avais au début n'était pas la vraie somme
car on
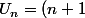(n+2))
et la somme de k(k-1) de 2 à n vaut
)
et la suite qui traduit la somme est plutôt
Sn= Somme de
)
de 2 à n dont je n'arrive pas rien à trouver
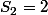
;
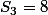
;
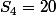
;
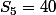
j'ai aussi pas compris comment la polynôme peut nous donner la forme
(n+1)}{3})
ou peut-être qu'il donne juste la somme sous forme :
)
?
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 10 Mai 2014, 19:28
par Gonra » 10 Mai 2014, 19:28
on a aussi
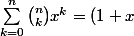^n)
en dérivant 2 fois et en posant x = 1 on a
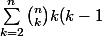=n(n-1)(1+1)^{n-2}=n(n-1)2^{n-2))
cela voudrait dire que

pour n => 2 ou bien je suis à l'ouest ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Mai 2014, 20:56
par zygomatique » 10 Mai 2014, 20:56
je ne vois pas l'intérêt de focaliser sur les indices ....
que veux tu calculer exactement ?
la somme des k(k + 1) de k = 0 jusqu'à n ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 11 Mai 2014, 09:37
par Gonra » 11 Mai 2014, 09:37
que veux tu calculer exactement ?
la somme des k(k + 1) de k = 0 jusqu'à n ?
la somme de k(k-1) de 2 à n

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Mai 2014, 12:07
par zygomatique » 11 Mai 2014, 12:07
donc la somme des k(k + 1) de 0 à n - 1 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Mai 2014, 10:40
par deltab » 13 Mai 2014, 10:40
Bonjour.
Gonra a écrit:bonjour
on m'a aussi parler d'une polynôme qu'il fallait dériver qui donne directement la somme
Le polynôme
)
en question est
=\sum_{k=2}^n \text{ }x^k=....)
(expression à simplifier) dont la dérivée seconde donne bien pour

la somme
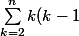)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Mai 2014, 17:34
par zygomatique » 13 Mai 2014, 17:34
certes oui .... et alors ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
