Convergence suite et série

[RyanB]

Bonjour, je vais essayer de recopier le sujet de la manière la plus compréhensible. (j'écrirai KUn pour la série de terme général Un)

Soit (Un), (Vn), deux suites de reels et on suppose:
Un> 0
La série KVn est absolument convergente
Pour tout entier n, Un+1/Un=1+a/n+vn

On pose Xn=ln [ ((n+1)^a Un+1)/ (n^a Un) ]

Il y a deux questions de l'exercice auxquelles je n'arrive pas a répondre.

1) Montrer que la série KXn converge si et seulement si la suite (n^a Un) converge
2) Montrer que la série KVn² converge

Merci d'avance pour vos éléments de réponse

Ryan

[arnaud32]

utilises le fait que ln(u*v)=ln(u)+ln(v)

[RyanB]

Êtes vous sur?

J'ai déjà essayé de passer par là, mais ca fait disparaître la suite (n^a Un)

J'ai aussi pensé à utiliser le fait que (n^a Un)>0 et donc converge si et seulement si
((n+1)^a Un+1)/(n^a Un) tend vers u avec u appartenant à [0,1[ mais je n'ai pas réussi à conclure a la convergence de xn

[adrien69]

(n^a Un)>0 et donc converge si et seulement si
((n+1)^a Un+1)/(n^a Un) tend vers u avec u appartenant à [0,1[

Ça c'est méga faux !

La série de terme général 1/n² converge, et pourtant n²/(n+1)² tend vers 1.

[adrien69]

Sinon Arnaud a raison :
ln(a/b)=ln(a)-ln(b) te ramène à une série téléscopique avec laquelle il est immédiat de conclure pour la première question.

[RyanB]

En effet, c'est le fait que u appartienne a [0,1[, qui fait que la série de terme général Un converge, mais la réciproque n'est pas toujours vraie.

D'accord je vais essayer comme ça, merci

[RyanB]

J'ai compris. Le problème c'est que je ne connaissais pas très bien les séries télescopique,

Une idée pour la question 2)?

[adrien69]

Ouep.

Si |x|<1, tu peux comparer comment |x| et |x|² ?

[RyanB]

Si je ne dis pas de bêtise,

KVn Converge absolument, donc |vn|->0 donc il existe un n a partir duquel |vn|<1, donc vn²<|vn|

Et donc par comparaison, K vn² converge.

[adrien69]

Voilà. Du fait de la positivité de Vn².

[RyanB]

Merci beaucoup.

[RyanB]

Je reviens vers vous car j'ai encore un problème, décidement j'ai vraiment du mal avec l'étude des suites et séries.

Soit fn(x)=e^(-x Rac(n)) (où rac(n) et la racine carrée de n).

J'ai déjà montré que la série Kfn convergeait sur ]0,+oo[

Je dois maintenant montrer que f, la somme de cette série, est continue sur ]0, +oo[. Je sais qu'il suffit de montrer que fn converge uniformément vers f sur ]0, +oo[, pour montrer que f est continue, sauf que je ne connais pas f, donc je ne sais pas comment m'y prendre.

[bentaarito]

regarde la limite de

[bentaarito]

Regarde la somme de la série de terme

[RyanB]

J'avais pensé à ça, j'obtiens une série géométrique de raison e^-x, et j'obtiens directement sa somme. Ensuite je n'ai plus qu'à montrer que le sup|fn(x)-f(x)| tend vers 0 quand n tend vers l'infini.

Mais est ce que la somme de fn et la meme que fn²? si oui pourquoi?

[deltab]

Bonsoir

J'avais pensé à ça, j'obtiens une série géométrique de raison e^-x, et j'obtiens directement sa somme. Ensuite je n'ai plus qu'à montrer que le sup|fn(x)-f(x)| tend vers 0 quand n tend vers l'infini.
Mais est ce que la somme de fn et la meme que fn²? si oui pourquoi?

La réponse est non! La série harmonique diverge mais la série formée par les termes 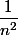converge.
Tu semple confondre entre la suite (f_n) et la série \sum f_n(x)

Ensuite je n'ai plus qu'à montrer que le sup|fn(x)-f(x)| tend vers 0 quand n tend vers l'infini.

Tu avais noté par f(x) la somme de la série et non la limite simple de la suite .

Pour l'étude de certaines propriétés de la somme d'une série de fonctions, on n'a nul besoin d'expliciter .
On n'a pas la convergence uniforme de cette série sur , tu peux dire pourquoi?
Essaies plutôt de montrer que la série converge normalement sur tout intervalle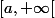 où a>0

[RyanB]

Je suis désolé de me tromper autant et vous remercie pour votre patience, j'ai vraiment du mal avec cette matière.

Je n'avais même pas pensé à utiliser la convergence en norme.

fn(x)=e^(-x rac(n)) est décroissante sur [a,+oo[, donc son sup est e^(-a rac(n))

De plus K (e^(-a rac(n))) < K ((e^-a)^n) qui converge donc K sup fn(x) converge.

Donc la série est normalement convergente et donc elle converge uniformement vers f . Ce qui implique la continuité de f

C'est bien ça?