Exercice de maths 1ereS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cookandeffy
- Messages: 3
- Enregistré le: 30 Avr 2014, 15:43
-
 par cookandeffy » 30 Avr 2014, 15:48
par cookandeffy » 30 Avr 2014, 15:48
Bonjour a tous , j'ai un dm de maths a faire sur les fonctions dérivées , et je ne trouve vraiment pas comment résoudre l'exercice 1 , ce serait super sympa si quelqu'un pouvait m'aider un peu
 Expliquez de deux façons differentes pourquoi , lorsque h est proche de 0 , l'approximation
Expliquez de deux façons differentes pourquoi , lorsque h est proche de 0 , l'approximation
f(a+h)= f(a)+hf'(a) semble légitime . voila , merci beaucoup d'avance !

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 30 Avr 2014, 16:09
par capitaine nuggets » 30 Avr 2014, 16:09
Salut !
cookandeffy a écrit:Bonjour a tous , j'ai un dm de maths a faire sur les fonctions dérivées , et je ne trouve vraiment pas comment résoudre l'exercice 1 , ce serait super sympa si quelqu'un pouvait m'aider un peu
 Expliquez de deux façons differentes pourquoi , lorsque h est proche de 0 , l'approximation
Expliquez de deux façons differentes pourquoi , lorsque h est proche de 0 , l'approximation
f(a+h)= f(a)+hf'(a) semble légitime . voila , merci beaucoup d'avance !
Salut !
- Quel est la définition du nombre dérivée d'une fonction

dérivable en

?
- Que se passe-t-il lorsque
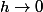
pour
)
? Pour
+hf'(a))
?
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 30 Avr 2014, 19:04
par paquito » 30 Avr 2014, 19:04
On a( f(a+h)-f(a))/h qui a pour limite f'(a) quand h ->o, donc si h est proche de 0,( f(a+h)- f(a))/h est proche de f'(a), donc f(a+h)=f(a)+hf'(a) doit être une bonne approximation. D'autre par, on peut considérer qu'au voisinage de a, que la tangente est pratiquement confondue avec la courbe et donc que pour h assez petit, ((a+h); f(a+h)) est sur la tangente, ce qui donne f(a+h)pratiquement=f'(a)h+f(a).
-
cookandeffy
- Messages: 3
- Enregistré le: 30 Avr 2014, 15:43
-
 par cookandeffy » 05 Mai 2014, 17:20
par cookandeffy » 05 Mai 2014, 17:20
D'accord , c'est a peu près ce que j'ai fait .
Merci beaucoup :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités