Polynomes de Tchébychev
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Drine
- Messages: 1
- Enregistré le: 12 Sep 2006, 18:29
-
par Drine » 12 Sep 2006, 18:42
Bonjour tout le monde, voilà j'ai besoin de votre aide pour cet exercice que je n'arrive pas à faire...
Pour tout n entier naturel et pour tout réel x on pose Tn (cosx)=cos (nx)
Cette formule définit une fonction polynome Tn.
Par exemple pour tout n , Tn est de degré n et a exactement n racines dans l'intervalle [-1;1]
POur 1 En déduire les 5 premiers polynomes de Tchebytchev.
Vérifier que T5(x)=2xT4(x)-T3(x)
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
par nada-top » 12 Sep 2006, 19:34
tu veux dire
alors pour
et
je crois que tu sais faire .
pour
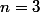
 = cos(3x) =..)
alors pour trouver il suffit de linéariser en utilisant les formules d'addition avec
=cos(2x+x))
puis utiliser
 = 1-cos^2(x))
pour
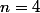
 = cos(4x) = cos(2(2x))=)
...
pour
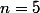
 = cos(5x) = ...)
tu utilises les formules d'addition .
Sinon si tu connais les complexes c fini ...
il suffit de voir que :
 = Re[(cosx + isinx)^3])
, tu dévellope
^3)
et tu isole la partie réelle .
idem avec
=Re[(cosx +isinx)^5])
et
=Re[(cosx +i sinx)^4])
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
