Arithmétique pgcd/ppcm
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
par Pierre.S » 23 Avr 2014, 15:44
Bonjour à vous !
J'ai un exo darithmétique qui fait de la résistance.
Le problème consiste à résoudre dans
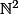
l'équation diophantienne :
(E)
^2 = 147ppcm(x,y))
Je pose (x,y) solution de (E),
)
,
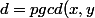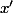
et
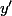
tel que
et
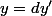
L'exercice nous guide pour montrer que
^2 | 147x'y')
et donc que
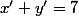
Je dois maintenant trouver les solution de (E) mais j'avoue ne pas savoir quoi faire...
En vous remerciant.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
par nodjim » 23 Avr 2014, 18:58
On a déja le couple (12,30) qui est solution. C'est possible qu'il n'y en ait pas d'autres.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 23 Avr 2014, 19:08
Salut,
Partant de là :
^2 = 147ppcm(x,y)\)
tu as dû en déduire que
^2 = 3.7^2.x'y'\ (E')\)
qui implique effectivement que
^2 | 3.7^2\)
vu que
)
est premier avec
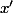
et avec
.
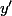
Cela signifie que
et donc que
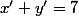
vu que
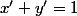
est absurde (je suppose que tu cherche les solutions entière strictement positives)
Maintenant, si tu réinjecte ça dans l'équation (E'), ça te donne
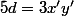
donc x' (ou y', mais c'est pareil) est divisible par 5 et comme x'+y'=7, ça ne laisse pas trop de possibilités...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
par Pierre.S » 24 Avr 2014, 19:52
Je vous remercie bien j'ai finalement trouvé la réponse en utilisant les conditions :
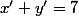
=1)
(En isolant
on obtient
et je ne cherche que les solutions entières positives)
Après résolution on obtient comme solutions :
,(12,30))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
