Equation fonctionnelle.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 27 Aoû 2006, 02:12
par nuage » 27 Aoû 2006, 02:12
Pour faire remonter le sujet.
Je verrais ça demain. Si j'ai le temps, mais ça m'interesse.
A+
-
polymathematic
- Membre Naturel
- Messages: 44
- Enregistré le: 15 Aoû 2006, 08:19
-
 par polymathematic » 27 Aoû 2006, 02:31
par polymathematic » 27 Aoû 2006, 02:31
ca fai un moment que j n suis pa revenu ici
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 28 Aoû 2006, 02:26
par nekros » 28 Aoû 2006, 02:26
Salut,
Si ça vous intéresse, d'autres matheux se sont penchés sur ce problème : cliquer
ici Pas de solution finale non plus

A+
-
geta
- Messages: 5
- Enregistré le: 06 Aoû 2006, 19:51
-
 par geta » 12 Sep 2006, 06:10
par geta » 12 Sep 2006, 06:10
Et si on mettait les problèmes non encore résolus dans un sous morceau du forum spécialement prévu à cet effet ?
:id:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 12 Sep 2006, 08:41
par nox » 12 Sep 2006, 08:41
ca peut etre une bonne idée (mais je sais pas si c'est super gérable pour les admins...enfin bon ca coute rien de proposer)
Postes un truc pour suggérer ca dans "à propos de ce site" on verra bien
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 12 Sep 2006, 15:40
par B_J » 12 Sep 2006, 15:40
si on suppose que f est derivable alors :
f(x+1)=f(x)+f(1/x) en derivant et en utilisant f(x+1)=f(1+1/x) on aura :
f'(x+1)=(-1/x²)f'(1+1/x) = (-1/x²)f'(x+1) => f'(x+1)=0 pour x non nul
donc f=cte
or f(1)=f(2)=2f(1) => f=0 pour tout x
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 12 Sep 2006, 17:12
par alben » 12 Sep 2006, 17:12
B_J a écrit:si on suppose que f est derivable alors :
f(x+1)=f(x)+f(1/x) en derivant et en utilisant f(x+1)=f(1+1/x) on aura :
f'(x+1)=(-1/x²)f'(1+1/x) = (-1/x²)f'(x+1) pour x non nul
donc f=cte
or f(1)=f(2)=2f(1) => f=0 pour tout x
Bonsoir,
Je ne retrouve pas ton résultat.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 12 Sep 2006, 18:20
par Imod » 12 Sep 2006, 18:20
Un petit mot pour dire que je ne peux pas suivre B_J dans sa logique : f(x+1)= f(1 + 1/x) donc f'(x+1) = f'(1 + 1/x) . J'ai essayé sur le site que signale nekros de montrer qu'il existait une infinité de solutions au problème . Parmi elles il y en a sans doute certaines qui sont dérivables voire plus .
Imod ( ie : Domi mais le pseudo est déjà pris :cry: )
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 01:50
par B_J » 13 Sep 2006, 01:50
on a f'(1+1/x)=f'(1+x) mais aussi [f(1+1/x)]' =(1+1/x)' *f'(1+1/x) ...
( derivee d'une fonction composee )
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 13 Sep 2006, 06:36
par alben » 13 Sep 2006, 06:36
B_J a écrit:on a f'(1+1/x)=f'(1+x)
En vertu de quoi????
B_J a écrit:mais aussi [f(1+1/x)]' =(1+1/x)' *f'(1+1/x) ...
d'accord, c'est la seule chose vraie me semble-t-il
Sur le fond, je ne pense pas que la fonction soit identiquement nulle Je n'ai pas encore eu le temps de suivre dans le détail la construction proposée par Domi=Imod mais je serai très curieux de voir la tête d'une fonction qui satisfasse à la relation
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 12:34
par B_J » 13 Sep 2006, 12:34
alben a écrit:En vertu de quoi????
ben si f=g alors f'=g' non ?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 12:43
par B_J » 13 Sep 2006, 12:43
ex :
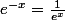
donc j'ai le droit d'ecrire que
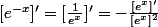
non ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 13 Sep 2006, 12:55
par alben » 13 Sep 2006, 12:55
ex : cos(x)=cos(-x)
donc -sin(x)=-sin(-x) d'après toi :zen:
L'égalité de deux fonctions signifie qu'elles se coupent, pas qu'elles sont tangentes !
Ton exemple marche parce que tes deux fonctions ne sont en fait que deux écritures de la même.
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 13:02
par B_J » 13 Sep 2006, 13:02
attention
cos(x)=cos(-x) =>cos'(x)=cos'(-x)
mais cos'(-x) = (-x)'*cos'(-x)=-1*-sin(-x)=sin(-x)=-sinx
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 13:03
par B_J » 13 Sep 2006, 13:03
alben a écrit:ex : cos(x)=cos(-x)
donc -sin(x)=-sin(-x) d'après toi :zen:
.
n'oublie que tu derives une fonction composee
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 13 Sep 2006, 13:06
par nox » 13 Sep 2006, 13:06
alben a écrit:ex : cos(x)=cos(-x)
donc -sin(x)=-sin(-x) d'après toi :zen:
je crains que (cos(-x))' = sin(-x) = -sin(x)
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 13 Sep 2006, 13:07
par nox » 13 Sep 2006, 13:07
C'est vrai que ca me semble bon...
Si f(x) = g(x) pour tout x on a bien f' = g' aussi...je vois pas de contre exemple...puisque comme tu dis g n'est qu'une autre écriture de f
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 13 Sep 2006, 13:07
par B_J » 13 Sep 2006, 13:07
alben a écrit:L'égalité de deux fonctions signifie qu'elles se coupent, pas qu'elles sont tangentes !
.
ah bon
pourtant tu ecris
=cos(-x))
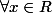
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 13 Sep 2006, 13:39
par Flodelarab » 13 Sep 2006, 13:39
Je vois pas comment 2 fonctions définies identiquement pourrait avoir des dérivées différentes....
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 13 Sep 2006, 13:47
par alben » 13 Sep 2006, 13:47
Tu m'embrouilles, tu t'embrouilles...
Soyons précis : tu prétends qu'à partir de f(x+1)=f(1+1/x) tu peux déduire f'(x+1)=f'(1+1/x)
C'est faux
Il ne s'agit pas de f=g pour tout x mais de (foh)(x)=(fok)(x). Il s'agit de fonctions composées et tu as seulement (foh)'=(fok)' donc f'(h(x))h'(x)=f'(g(x))k'(x).
Mais h'(x)=1 et k'(x)=(-1/x²)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités

