Loi normale multivariée

[greg974974]

Bonjour,

Je dispose d'une variable aléatoire : un point situé dans l'espace de coordonnées (X, Y, Z).

Mon but est de connaitre l'ellipsoïde d'erreur autour de celui-ci.

Je rappelle la loi normale bivariée (on ne considère que les composantes X et Y) :

f(x, , , ) = 1/(2..1.2).e^-(1/2.(1-;)^2)).((x1-;)1)^2/;)1^2-(2..(x1-;)1).(x2-;)2))/(;)1.2)+(x2-;)2)^2/;)2^2)

http://lpsc.in2p3.fr/collot/cours/Proba.pdf

Mon cours me donne les paramètres des ellipses qui correspondent à l'équiprobabilité de cette fonction :

a = (s0.K/sqrt(2)).sqrt(;)1^2+;)2^2+sqrt((;)1^2+;)2^2)^2+4.12^2+))
b = (s0.K/sqrt(2)).sqrt(;)1^2+;)2^2-sqrt((;)1^2+;)2^2)^2+4.12^2+))
= 2.12/(;)1^2-;)3^2) --angle entre Ox et a--

Je dois donc utiliser la loi normale multivariée avec 3 variables...

La voici :



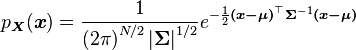
J'ai 2 problèmes : je ne sais pas comment passer de la loi normale bivariée aux paramètres des ellipses... Et je ne sais pas appliquer cela a la loi normale multivariée.

Merci d'avance pour votre aide :lol3:

[forhekset]

Bonjour,

Le resultat que tu donnes se trouve en diagonalisant la matrice de variance-covariance.
Les vecteurs propres te donneront les axes de ton ellipses (la racine des valeurs propres te donneront la longeur relative des axes avec un facteur d'echelle que tu choisis (s0) ).
En fait, tu cherches une base dans laquelle tu n'auras plus de covariance ; )
Le resultat en 3D s'obtient de la meme maniere.

[greg974974]

D'accord, du coup je dispose d'une matrice :

| 11 12 13 |
| 21 22 23 |
| 31 32 33 |

-;).I :

| 11-;) 12 13 |
| 21 22-;) 23 |
| 31 32 33-;) |

det(;) -;).I) = (;)11-;)).((;)22-;)).(;)33-;))-;)32.23)-;)12.(;)21.(;)33-;))-;)31.23)+;)13.(;)21.32-;)31.(;)22-;)))

Seulement, quand je développe, j'obtiens un polynôme de degré 3. J'ai essayé de calculer les racines d'un tel polynôme suivant la méthode de Cardan :

http://fr.wikiversity.org/wiki/%C3%89quation_du_troisi%C3%A8me_degr%C3%A9/M%C3%A9thode_de_Cardan

http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Cardan

Mais voila, les racines dont des nombres complexes... Comment il faut faire du coup?

Une fois cette étape faite, je pourrai facilement calculer les vecteurs propres en utilisant Gauss-Jordan :

| 11.Xi 12 13 |___|x|___|0|
| 21 22.Xi 23 |_x_|y|_=_|0|
| 31 32 33.Xi |___|z|___|0|


avec Xi une des trois racines du polynôme, le vecteur (x, y, z) le vecteur propre...

Mais pour le moment je ne vois pas comment traiter ce polynôme du 3ème degré...

[greg974974]

Je pourrais utiliser la technique de la solution évidente mais je voudrais automatiser... donc je peux pas...

[forhekset]

Desole pour le retard ( vacances )

Comme ta matrice de covariance est symetrique defini positive, tu sais qu'elle est diagonalisable dans R avec des vp strictement positives. ( theoreme spectrale )

Je n'ai fait que le calcul en 2D , mais a priori tu devrais tomber sur des vp reelles positives en calculant les racines du polynome caracteristique.

[houD]

je travaille avec une loi normale multivariée avec X suit N(mu,;)), mu représente la moyenne et la matrice de covariance
pour une loi normale avec X suit (mu,;)²) avec mu la moyenne et ² la variance , on a u(k)=mu_0+delta*;)_0+beta(k-t)*;)_0

est ce que dans le cas multivariée , cette formule peut être égale à :

u(k)=mu_0+delta*;)_0+beta(k-t)*;)_0

je dois utiliser la loi normale multivariée mais je ne sais comment l'appliquer sur cette formule ?
merci d'avance pour votre aide