Bonsoir,
Je coince sur ceci:
Calculer les limites suivantes:
1)Lim(x tend vers 8) (x^(1/3)-2)/((x+19)^(1/3)-3)
2)lim(x tend vers 1)(;)x-1)/(x^(1/3)-1)
Limite
6 messages
- Page 1 sur 1
Bonsoir
pour 1)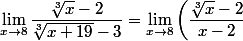 \left(\dfrac{x-8} {\sqrt[3]{x+19}-3}\right)) . Que reconnait-on dans les limites des 2 derniers facteurs?
. Que reconnait-on dans les limites des 2 derniers facteurs?
pour 2) essaies d'adopter la même démarche.
PS: Ceci revient en fait à utiliser la règle de l'Hôpital, règle qui apparemment n'est plus au programme.
.magy a écrit:Bonsoir,
Je coince sur ceci:
Calculer les limites suivantes:
1)Lim(x tend vers 8) (x^(1/3)-2)/((x+19)^(1/3)-3)
2)lim(x tend vers 1)(;)x-1)/(x^(1/3)-1)
pour 1)
pour 2) essaies d'adopter la même démarche.
PS: Ceci revient en fait à utiliser la règle de l'Hôpital, règle qui apparemment n'est plus au programme.
Salut,
A chacun ces méthodes, mais perso,. avant même de commencer à réfléchir, lorsque j'ai x->8, je pose x=8+h avec h->0 (idem lorsque x->1 où je pose x=1+h).
La raison ?
Les seules formules de D.L. que je connais sont avec la variable qui tend vers 0 et la définition de la dérivée que je préfère, c'est=\lim_{h\to 0}\frac{f(x_o+h)-f(x_o)}{h})
A chacun ces méthodes, mais perso,. avant même de commencer à réfléchir, lorsque j'ai x->8, je pose x=8+h avec h->0 (idem lorsque x->1 où je pose x=1+h).
La raison ?
Les seules formules de D.L. que je connais sont avec la variable qui tend vers 0 et la définition de la dérivée que je préfère, c'est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
