bonjour à tous j aimerai vous demander de l'aide pour un développement limité cela fait un peu plus de quelque semaine que je n'arrive pas à trouver cette limite
soit f(x)=1/(2(1-racine(x))) - 1/(3(1-x^(1/3)))
étudier la limite de f(x) quand x tend vers 1
merci d'avance pour toutes aides
étude de limite
6 messages
- Page 1 sur 1
itachi92 a écrit:bonjour à tous j aimerai vous demander de l'aide pour un développement limité cela fait un peu plus de quelque semaine que je n'arrive pas à trouver cette limite
soit f(x)=1/(2(1-racine(x))) - 1/(3(1-x^(1/3)))
étudier la limite de f(x) quand x tend vers 1
merci d'avance pour toutes aides
Tu cherches la limite quand h tend vers 0 de:
Connaissant le développement limité en 0 de
la suite devrait découler facilement... non?
aide
Aristarque a écrit:Tu cherches la limite quand h tend vers 0 de:
Connaissant le développement limité en 0 de
la suite devrait découler facilement... non?
je considère donc deux fonctions
g(h)=
et
y(h) =
je dérive donc chaque expression une fois mais je trouve
g'(h)=-1/(4(racine(1+h))*((1-racine(1+h))^2)
y'(h)=-1/(9(1+h)^(-2/3)*((1-[1+h]^(1/3))^2)
mais après je n'arrive pas a finir car daprès la formule de taylor je dois faire le DL de g(h)=g(0)+g'(0)*x mais g(0) n'est pas déterminer et la même chose pour y(0). merci pour votre explication.(ps je ne maîtrise pas le langage tex)
Bonsoir.
Tu t'es mal pris concernant l'utilisation des DL.

}=-\dfrac{2}{h}\times \dfrac{1}{1+...}=-\dfrac{2}{h}\times (1+.....))
Je me suis limité à l'ordre 1 dans ce qui précède mais ça ne permettra pas de conclure, il faudra aller à l'ordre 2.
PS: Écrire est erroné car
est erroné car 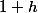 tend vers
tend vers  quand
quand  tend vers
tend vers  ét non vers
ét non vers 
itachi92 a écrit:je trouve en fessant le DL de
hg(h)=2(1-[1+h]^(1/2))+h([1+h]^(-1/2))/4(1-[1+h]^(1/2))²
hy(h)=3(1-[1+h]^(1/3))+h([1+h]^(-2/3))/9(1-[1+h]^(1/3))²
mais après je ne c pas quoi faire.
Tu t'es mal pris concernant l'utilisation des DL.
Je me suis limité à l'ordre 1 dans ce qui précède mais ça ne permettra pas de conclure, il faudra aller à l'ordre 2.
PS: Écrire
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
