Limite d'une somme ....

[Pierre.S]

Bonjour,

Une question d'un exercice correspondant au chapitre des intégrales (de terminale S donc) me demande de déterminer la limite de la suite

Pour cela l'exercice m'amène à démontrer que l'énoncé dit ensuite simplement "en déduire la limite lorsque p tend vers plus l'infini" pour ensuite faire un algorithme qui approche la limite de la suite.

Le problème est que en ayant une simple inégalité je ne voit pas comment je pourrais y arriver ....

Je vous remercie.

[Ben314]

Salut,
A mon avis, ce qu'on t'a demandé de démontrer, c'est plutôt un truc du style que,
Pour tout entier , on a
Puis de faire la somme de ces inégalité pour k entre ??? et ??? : à droite ça se "télescope" clairement.

[Pierre.S]

Salut,
A mon avis, ce qu'on t'a demandé de démontrer, c'est plutôt un truc du style que,
Pour tout entier , on a
Puis de faire la somme de ces inégalité pour k entre ??? et ??? : à droite ça se "télescope" clairement.

Oui en fait j'ai fait une erreur dans mon premier message désolé ...

Je dois déduire la limite à partir de

[Pierre.S]

Si ça peut t'éclairer voila le plan de l'exo :

1.a Montrer que Un est croissante
1.b Montrer que
1.c Que peut-on en conclure sur la suite ?

2.a Vérifier pour que pour tout K \ {0,1} on a :
2.b En déduire que pour tout entiers on a :

Et en déduire la limite lorsque p tend vers l'infini.

[paquito]

Le petit problème, c'est qu'on ne sait pas calculer lim(k=1 à+inf)(sigma)1/k^3, donc, comment utiliser une limite qui existe, mais qu'on ne connait pas?

[Pierre.S]

Le petit problème, c'est qu'on ne sait pas calculer lim(k=1 à+inf)(sigma)1/k^3, donc, comment utiliser une limite qui existe, mais qu'on ne connait pas?

Effectivement après quelques recherches j'ai vu que cette limite était inconnu. Du coup je me suis dis que c'était pour ça qu'on calculer la limite de la somme uniquement de n+1 à p et pas de 1 à p ... Mais j'avoue que j'ai du mal à voir.

[Ben314]

Ce que tu en déduit, c'est "tout con" :
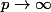
- à gauche de l'inégalité, tu as qui tend vers lorsque (avec fixé) où L est la limite de la suite .
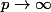
- à droite de l'inégalité tu as qui tend vers lorsque (avec fixé)
Tu en déduit donc que , c'est à dire que

D'un autre coté, comme la suite est clairement croissante, tu as aussi et avec l'inégalité çi dessus, ça te dit que est compris entre et .

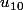
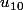
Donc si avec une machine ou un ordi tu calcule par exemple , tu en déduira que est entre et ce qui signifie que tu aura la valeur de à moins de un centième prés...

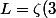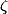
Bon, aprés, effectivement, la valeur exacte de , on ne sait pas l'exprimer avec les fonctions "usuelles" (celle standards sur une machine), mais on peut par exemple écrire que où est une fonction "classique" (mais moins "usuelle" que celle qu'il y a sur une machine à calculer "de base").
D'un autre coté, la valeur exacte de , on sait pas trop l'exprimer non plus sans utiliser la fonction logarithme...

[Pierre.S]

J'ai plus ou moins fais ça mais j'avoue que je m'attendais à une limite plus "explicite" mais en fin de compte c'est le plus juste. Je vous remercie.

Oui j'ai vu en faisant des recherches que ce genre de fonction était utilisés, je n'ai pas tout compris mais le calcul des sommes et des produits m'intéresse beaucoup et



est-ce que c'est ça ?

Enfin merci encore et bonne soirée.

[Ben314]

Oui, c'est parfaitement ça (en tout cas, pour a>1).
Ça explique que, au niveau théorique, si on écrit que , ça fait pas bien avancer le "schmilblick" vu que c'est la définition de la fonction zeta...
Mais en fait on peut rapprocher ça de l'écriture de qui est du même style : c'est pas super pertinent vu que c'est quasiment la définition de la fonction logarithme...
Sauf qu'en fait, ma fonction logarithme, bien qu'on ne sache pas vraiment calculer exactement les valeurs qu'elle prend par exemple sur les entier, on en connait des tas de propriétés qui font qu'on a l'impression que l'expression , c'est un truc parfaitement "acceptable" comme réponse à une question...

[paquito]

Oui, c'est parfaitement ça (en tout cas, pour a>1).
Ça explique que, au niveau théorique, si on écrit que , ça fait pas bien avancer le "schmilblick" vu que c'est la définition de la fonction zeta...
Mais en fait on peut rapprocher ça de l'écriture de qui est du même style : c'est pas super pertinent vu que c'est quasiment la définition de la fonction logarithme...
Sauf qu'en fait, ma fonction logarithme, bien qu'on ne sache pas vraiment calculer exactement les valeurs qu'elle prend par exemple sur les entier, on en connait des tas de propriétés qui font qu'on a l'impression que l'expression , c'est un truc parfaitement "acceptable" comme réponse à une question...

En fait, on sait trouver quand k est pair; le moyen le plus simple est d'utiliser le développement en série de FOURIER avec une fonction bien choisie.

[Pierre.S]

Ok d'accord je vois le truc. Ça a vraiment l'air super intéressant. Je penses que mes études me conduiront étudier ce genre de chose enfin j’espère mais pour l'instant je ne connais pas du tout ce qu'est une série de FOURIER même si j'en ait entendu parler. D'ailleurs je ne sais même pas ce qu'est une série tout court ^^

Enfin bon après finis l'exo l'algorithme m'approche à environ 1.20 ce qui semble acceptable vu les approximations que j'ai pu trouver sur internet.

Je vous remercie donc. Un forum très agréable en tout cas. Bonne soirée.