Demonstration d'une inégalité.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
par Pierre.S » 13 Avr 2014, 10:26
Bonjour.
Je m'arrache actuellement les cheveux depuis des heures sur une question d'un DM (mais j'ai beaucoup de temps pas d'inquiétude.).
Le problème consiste à prouver que pour tout
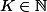
\ {0,1} on a :
^2}-\frac{1}{k^2})
J'ai essayé par récurrence mais sans arriver à aboutir à une hérédité (lhypothèse de récurrence n'est pas évidente à utiliser de mon point de vue). J'ai tenté toutes les autres idées qui me venaient en tête mais sans résultat pour l'instant...
En vous remerciant par avance.
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
par Pierre.S » 13 Avr 2014, 10:42
Hum je viens de me rendre compte que j'avais fais une erreur lors de ma tentative de l'étude du signe de la fonction :
 = \frac{1}{(k-1)^2}-\frac{1}{k^2} - \frac{1}{k^3})
définit sur ]1,
[
En mettant tout sur le même dénominateur on obtient :
=\frac {k^3-(k-1)^3}{k^3(k-1)^2})
Avec
^2>0)
car
^2>0)
car c'est un carré et k>0 et
car x>0
Donc le signe de f dépend uniquement du signe du numérateur or
^3)
sur
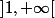
On en déduit
^3>0)
donc f>0 ce qui permet de conclure que pour tout
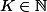
\ {0,1} :
La démonstration serait-elle valable ?
En vous remerciant et désolé si j'ai posté trop vite.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
par Sourire_banane » 13 Avr 2014, 10:45
Pierre.S a écrit:Bonjour.
Je m'arrache actuellement les cheveux depuis des heures sur une question d'un DM (mais j'ai beaucoup de temps pas d'inquiétude.).
Le problème consiste à prouver que pour tout
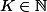
\ {0,1} on a :
J'ai essayé par récurrence mais sans arriver à aboutir à une hérédité (lhypothèse de récurrence n'est pas évidente à utiliser de mon point de vue). J'ai tenté toutes les autres idées qui me venaient en tête mais sans résultat pour l'instant...
En vous remerciant par avance.
Salut,
Remarque que
^2}-\frac{1}{k^2}=\[-\frac{1}{x^2}\]^k_{k-1}=2\int_{k-1}^{k}\frac{\mathrm{d}x}{x^3})
Edit : Pour k>1 bien sûr...
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
par Sourire_banane » 13 Avr 2014, 10:52
Pierre.S a écrit:Hum je viens de me rendre compte que j'avais fais une erreur lors de ma tentative de l'étude du signe de la fonction :
définit sur ]1,
[
En mettant tout sur le même dénominateur on obtient :
Avec
car
car c'est un carré et k>0 et
car x>0
Donc le signe de f dépend uniquement du signe du numérateur or
sur
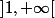
On en déduit
donc f>0 ce qui permet de conclure que pour tout
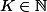
\ {0,1} :
La démonstration serait-elle valable ?
En vous remerciant et désolé si j'ai posté trop vite.
Ton calcul a l'air faux, mais c'est une bonne méthode.
J'arrive plutôt à
=\frac{k^2+k-1}{k^3(k-1)^2})
Le dénominateur est positif pour k>1 et le numérateur est positif pour k>1 aussi.
-
Pierre.S
- Membre Naturel
- Messages: 16
- Enregistré le: 13 Avr 2014, 10:10
-
par Pierre.S » 13 Avr 2014, 11:18
Sourire_banane a écrit:Ton calcul a l'air faux, mais c'est une bonne méthode.
J'arrive plutôt à
Le dénominateur est positif pour k>1 et le numérateur est positif pour k>1 aussi.
Très bien je te remercie. Je reverrai le calcul alors pourtant il me semblait correct mais peu importe je sais quoi faire dorénavant.
Bonne journée à toi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
