Urgent

[Anonyme]

salut tout le monde!je suis nouveau et j'ai tellement besoin d'aide.j'ai un problème sur une étude de convergence d'une séries. Je trouve aucune piste.Elle est de la forme 1/n(racine n-ième de n).Deso pour l'écriture mais je sais pas écrire les formes en maths ici.AIDE MOI SVP ET MER6 D'AVANCE

[chbichib]

je pense qu il suffit de passer a a log de l exponentiel de la somme et calculer la limite lorske n assez grand

[Anonyme]

oui c'est une option mais ske j’avais oublier de dire c'est qu'on a 2 théories a suivre pour le démontrer
- comparaison avec une séries de reimann
-par critère d'intégrale
a cause de cela que je sais pas quoi faire.ESK vous pouvez si possible de me donner les différentes forme selon vous qu'on peut ecrire ce series. mer6 pour la reponse

[MMu]

je pense qu il suffit de passer a a log de l exponentiel de la somme et calculer la limite lorske n assez grand

Ca t'avance à quoi le log de l'exponentielle ?! .. Any way ..
On observe que .. etc .. :zen:

[Robic]

À ton avis, cette série converge ou pas ? (C'est toujours utile de se poser la question : si on « sent » qu'elle diverge, pas besoin de se démener avec les critères de convergence...)

Le terme général est en .

S'il existait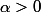 tel que , ce serait gagné : notre série serait majorée par la série des qui converge. Mais un tel 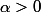n'existe pas puisque tend vers 0. Du coup, j'aurais tendance à penser que cette intégrale diverge. Ce n'est bien sûr pas une preuve (le critère de comparaison avec les intégrales de Riemann n'est pas une condition nécessaire et suffisante), mais disons que je sens mal la convergence. Quelque chose me dit que cette série ressemble à celle en 1/n.

Du coup, je suggère comme idée d'essayer de démontrer que le terme général est équivalent, à l'infini, à 1/n (alors ça prouvera la divergence). Je ne sais absolument pas si c'est le cas. En fait je ne sais pas faire l'exercice (pour l'instant !). Mais je sais que pour avoir une chance de trouver la réponse, il faut essayer des trucs et des machins (c'est comme ça qu'on finit par transformer le « pour l'instant » en « ça y est j'ai trouvé »)...

(Finalement j'ai essayé : ça marche. Le terme général est bien équivalent à 1/n. Donc «ça y est j'ai trouvé ».)

(1demada, ESK tu as vu lé ékivalents ?)

[Anonyme]

tu peut me donner les détailles de ton demos stp car je suis perdu ein.pour info il s'agit d'une séries divergente mais il suffit de montrer cela.mer6 robic

[zygomatique]

salut

passer par l'exponentielle et faire un dl ....

[Robic]

tu peut me donner les détailles de ton demos stp car je suis perdu ein.pour info il s'agit d'une séries divergente mais il suffit de montrer cela.mer6 robic

Réponds d'abord à ma question... (À quoi ça sert que je te donne ma démonstration si jamais tu n'as pas vu les équivalents ?)

Allez, je te donne quand même une indication : j'ai démontré que la racine énième de n est équivalente à 1 (c'est très facile à faire en passant à l'exponentielle).

[Anonyme]

1/n tu dit l'équivalent de cette séries mais la que je comprend pas comment tu démontre ça?ske je sais c'est a^{\frac 1n} =\exp\left(\frac 1n\ln a\right) .demontre le svp.MER6 d'avance

[zygomatique]

illisible ...

[Robic]

Pour la troisième fois : est-ce que tu as vu les équivalents ? (Tes messages me font douter, par exemple tu n'en parles pas lorsque tu listes les méthodes possibles.)

Peut-être que tu ne comprends pas ma question, alors je la refais : eske tu a vu les ékivalan ?
- Si oui, dis-moi oui.
- Si le mot ne te dis rien (les équivalents ? de quoi il parle ?) dis-moi non.

Si tu as vu les équivalents, voici la méthode :
- prouver que la racine énième de n est équivalente à 1 (c'est facile : il suffit de démontrer qu'elle tend vers 1 en utilisant la formule avec l'exponentielle),
- en déduire que le terme général de cette série est équivalent à la série des 1/n,
- conclure en invoquant la propriété comme quoi deux séries dont les termes sont équivalents sont de même nature.

Si tu n'as pas vu les équivalents, éventuellement je réfléchirai à une autre façon de faire (si j'ai le temps et l'envie - ça m'a l'air nettement plus compliqué s'il faut se passer des équivalents).

(Et surveille ton orthographe : dans « vous pouvez si possible de me donner les différentes forme » tu as oublié un s à « formes ».)

(Désolé, je suis moqueur, c'est pas bien. Mais quand on me tend le bâton... Et puis j'ai un excuse : j'ai aidé.)

[zygomatique]

puis on multiplie par n et on prend l'inverse ....

[Anonyme]

ok! mer6 a vous les amis. oui je comprend ske vous dite a propos de l' équivalent la réponse est oui.mer6 pour votre aide . :zen: