Intégrale trigonométirque

[smike2809]

Bonjour,

J'essaie en vain de résoudre cet exercice (si possible sans intégration par parties)



Merci pour votre patience

[low geek]

Bonjour (again ^^ )

que veux dire sec?

[chan79]

Bonjour (again ^^ )

que veux dire sec?

sec(x)=1/cos(x) je pense

[low geek]

Merci Chan je dormirai moins bête avec ça :)

Dans ce cas il n'y a rien de complexe dans cette intégrale:
on applique la formule tan(x)= sin(x)/cos(x) et sec(x)=1/cos(x) et tout roule ;)

[smike2809]

Merci Chan je dormirai moins bête avec ça

Dans ce cas il n'y a rien de complexe dans cette intégrale:
on applique la formule tan(x)= sin(x)/cos(x) et sec(x)=1/cos(x) et tout roule

Merci ca joue maintenant. Par contre si sec(x) + 1/cos(x) et arccos(x)=cos^-1(x) ce sont les mêmes fonctions?

[low geek]

Non ce ne sont pas les mêmes fonctions, arccos=cos^-1(x) est la fonction réciproque de cosinus; c'est a dire que arcos(cos(x))=x
sec(x)=cos^-1(x) est la fonction 1/cos(x)

Ce sont deux fonctions différentes qui ont la même notation il faut faire attention a pas les confondres ;)

[smike2809]

Non ce ne sont pas les mêmes fonctions, arccos=cos^-1(x) est la fonction réciproque de cosinus; c'est a dire que arcos(cos(x))=x
sec(x)=cos^-1(x) est la fonction 1/cos(x)

Ce sont deux fonctions différentes qui ont la même notation il faut faire attention a pas les confondres

Si je comprends bien:

sec(x)*cos(x)=1

et
cos(x)= y
arccos(y)=x

[low geek]

yep c'est ça ;)

[Black Jack]

sec²(x) - tan²(x) = 1/cos²(x) - sin²(x)/cos²(x) = (1 - sin²(x))/cos²(x) = cos²(x)/cos²(x) = 1

Et donc ...
*****

Mais attention à des choses comme ceci, (sans autres indications) :

cos(x)= y
arccos(y)=x

essaie par exemple avec x = -1 ou avec x = 5

:zen:

[LA solution]

je sais pas ce que vous faite.....
mais tan^2(x)=(sec^2)-1 et remplaca n par sa valeur on a: 1 et une primitive de 1 est x d ou l integrale est egale a pi sur 4

[low geek]

C'est ce que black jack a écris mais bon x)

[deltab]

Bonjour

Mais attention à des choses comme ceci, (sans autres indications) :

cos(x)= y
arccos(y)=x

essaie par exemple avec x = -1 ou avec x = 5

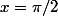
Même si l'égalité cos(x)= y est vérifiée, on n'a pas l'égalité arccos(y)=x, prendre ou mais par contre

[Black Jack]

Bonjour



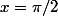
Même si l'égalité cos(x)= y est vérifiée, on n'a pas l'égalité arccos(y)=x, prendre ou mais par contre

C'est bien ce que voulait dire mon " (sans autres indications)"

On ne manipule pas les fonctions inverses (réciproques) sans les précautions d'usage sur les domaines.

:zen: