Complexe et rotation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 01:15
par quanti » 09 Avr 2014, 01:15
bonjour je suis en PTSI et j'aurai besoin d'aide pour une question.
le plan complexe est rapporté à un repère (o,i,j).
A un point M d'affixe z on associe la transformation
z'=f(z)=u^2*z+u-1
je dois déterminer l'ensemble des complexes pour lesquelles f est une rotation d'angle de mesure pi/2
j'ai essayer la relation z'=a*z
en remplacent par la relation donnée
j'obtient: u^2*z+u-1=e^ipi/2*z
mais je ne vois absolument pas ou cela me mène
merci d'avance pour votre aide
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Avr 2014, 02:15
par wserdx » 09 Avr 2014, 02:15
z'=a*z où |a|=1, est une rotation de centre 0
z'=a*(z-b) est une rotation de centre b.
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 02:22
par quanti » 09 Avr 2014, 02:22
wserdx a écrit:z'=a*z où |a|=1, est une rotation de centre 0
z'=a*(z-b) est une rotation de centre b.
donc il y a deux cas différent et dans le deuxième cas b est le centre de rotation si j'ai bien compris
mais je ne comprend pas d'ou vient le (z-b)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Avr 2014, 02:48
par wserdx » 09 Avr 2014, 02:48
ah oui désolé, une rotation de centre b c'est z'=a*(z-b)+b. (elle doit laisser b invariant)
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 02:55
par quanti » 09 Avr 2014, 02:55
je pensais que pour trouver le point invariant ,il fallait faire f(z)=z=w
bref j'ai utilisé w.
il y a ensuite une formule que je comprend pas
c'est: z'-w=a(z-w)
j'ai calculé w et a=e^ipi/é
j'ai remplace z' par la relation mais je tombe sur une équation du 4ieme degrés
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Avr 2014, 02:57
par wserdx » 09 Avr 2014, 02:57
Pour ton exercice, tu n'as juste pas tenu compte du fait qu'on ne t'impose pas le centre de la rotation.
Si tu choisis z'=az, tu ne considères que les rotations de centre 0.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Avr 2014, 03:02
par wserdx » 09 Avr 2014, 03:02
euh, je ne vois pas de 4ème degré.
Il suffit d'identifier:
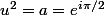
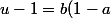)
La premiere équation donne u, la seconde donne b.
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 03:07
par quanti » 09 Avr 2014, 03:07
wserdx a écrit:Pour ton exercice, tu n'as juste pas tenu compte du fait qu'on ne t'impose pas le centre de la rotation.
Si tu choisis z'=az, tu ne considères que les rotations de centre 0.
d'accord j'ai compris mais on me demande l'ensemble des complexe qui,par la transformation, subirons
une rotation de pi/2
donc je dois aussi prendre en compte ceux qui n'ont pas comme centre de rotation O ?????
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Avr 2014, 03:17
par wserdx » 09 Avr 2014, 03:17
Euh, moi ce que j'ai compris de ton problème, c'est le paramètre

(complexe) qu'il faut déterminer
de telle sorte que
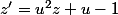
soit une rotation d'angle
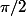
C'est bien ça?
Si oui, une rotation d'angle
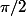
, s'exprime comme
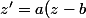+b)
avec
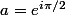
Il faut donc trouver b et u tels que
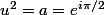
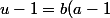)
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 03:41
par quanti » 09 Avr 2014, 03:41
wserdx a écrit:Euh, moi ce que j'ai compris de ton problème, c'est le paramètre

(complexe) qu'il faut déterminer
de telle sorte que
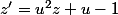
soit une rotation d'angle
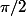
C'est bien ça?
Si oui, une rotation d'angle
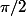
, s'exprime comme
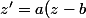+b)
avec
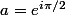
Il faut donc trouver b et u tels que
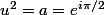
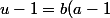)
je vais recopier l'énoncé pour que vous soyez sur mais je crois que c'est ça.
Le plan complexe est rapporté à un repère orthogonal (o,i,j)
on cosidére la transformation f(tild):P dans P qui au point M d'affixe z associe le point M' d'affixe z'.
:M dans M'
z'=u^2z+u-1. u est un paramètre appartenant à C
la question est : déterminer l'ensemble des complexes u pour lesquelles f(tild) est une rotation d'angle
de mesure pi/2.
Je crois que c'est bien ça .
merci bien pour ton aid :we: e

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Avr 2014, 07:38
par chan79 » 09 Avr 2014, 07:38
quanti a écrit:
la question est : déterminer l'ensemble des complexes u pour lesquelles f(tild) est une rotation d'angle de mesure pi/2.
il suffit de résoudre u²=i
on a deux valeurs et pour chacune, on peut calculer la position du centre, si c'est demandé
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 07:47
par quanti » 09 Avr 2014, 07:47
chan79 a écrit:il suffit de résoudre u²=i
on a deux valeurs et pour chacune, on peut calculer la position du centre, si c'est demandé
merci c'est ce que je viens de faire
j'obtient v2/2+v2/2i et -v2/2-v2/2i
et si j'ai bien compris je remplace u par les valeur trouvé dans l'expression de la transformation
z'=u^2+u-1

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Avr 2014, 07:52
par chan79 » 09 Avr 2014, 07:52
quanti a écrit:merci c'est ce que je viens de faire
j'obtient v2/2+v2/2i et -v2/2-v2/2i
et si j'ai bien compris je remplace u par les valeur trouvé dans l'expression de la transformation
z'=u^2+u-1
c'est ça.
L'ensemble des u qu'on te demande a comme éléments les deux nombres
)
et
)
-
quanti
- Messages: 9
- Enregistré le: 09 Avr 2014, 00:53
-
 par quanti » 09 Avr 2014, 07:59
par quanti » 09 Avr 2014, 07:59
chan79 a écrit:c'est ça.
L'ensemble des u qu'on te demande a comme éléments les deux nombres
)
et
)
merci pour votre aide vous m'avez bien débloqué :we: :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
(complexe) qu'il faut déterminer
soit une rotation d'angle
, s'exprime comme
avec
