Compact

[kammi]

bonjour,

Est ce que quelqu'un peut m'aider svp??

j'arrive pas a démontrer qu'un ensemble est compact

voila mon ensemble

U(nk)= {K L²[0,1] / K(x)= Co + (somme pour i=1...nk) [Ci.cos(2;)ix) + Di.sin(2;)ix)] avec [Co² + (1/2)(somme pour i=1...nk) (Ci²+Di²)] < ou = nk}

où les Ci et les Di sont respectivement les coéfficients de Fourier par rapport à la fonction cosinus et sinus

on a aussi comme donnée "K est est periodique de periode 1 et de norme<1"

[lionel52]

C'est un fermé borné d'un ev de dimension finie !!

[kammi]

C'est un fermé borné d'un ev de dimension finie !!

mais comment montrer la fermeture de cet ensemble? ''on est dans l'espace L²[0,1]''!!!

[Rha]

mais comment montrer la fermeture de cet ensemble? ''on est dans l'espace L²[0,1]''!!!

Bonsoir,

L'inégalité avec le est-elle large?

Si oui, en notant le sev de dimension finie de des polynômes trigonométriques (en ) de degré inférieur ou égal à , on peut montrer que .

[kammi]

Bonsoir,

L'inégalité avec le est-elle large?

Si oui, en notant le sev de dimension finie de des polynômes trigonométriques (en ) de degré inférieur ou égal à , on peut montrer que .

oui l'inégalité est large. mais je ne sais pas qu'est ce que je peux faire en utilisant cet ensemble!!

[Rha]

Je suppose que la norme sur est .

Alors cet ensemble est l'intersection de avec l'image réciproque de par .


La compacité d'une partie d'un evn ne dépend que de la partie et de la restriction de la norme à cette partie.
La partie est compacte dans si et seulement si elle l'est dans

[kammi]

Je suppose que la norme sur est .

Alors cet ensemble est l'intersection de avec l'image réciproque de par .


La compacité d'une partie d'un evn ne dépend que de la partie et de la restriction de la norme à cette partie.
La partie est compacte dans si et seulement si elle l'est dans

est ce que U(nk) est compact dans ??

[Ben314]

Salut,
Je comprend pas trop tes notation (principalement ton nk : c'est UNE variable que tu note nk ? c'est bizare comme truc...)

Ce que je crois comprendre de ton énoncé :

1) On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R (ou dans C ?) muni de la norme
.
2) Dans cet espace, on considère des parties de la forme :

où et
et ça donne l'impression que ce que toi tu considère, c'est les (ce qui personnellement me semble... pas très malin...)

Ta première question, ça semblait être "Est-ce que U(?,?) est compact" : là, c'est clair et on se fout des ? : c'est un fermé borné dans un e.v. de dim finie : c'est un compact.

La deuxième semble être "est-ce que la réunion des est compacte" et c'est là que le fait de prendre rend le truc "débile" : la réunion des n'est clairement pas bornée donc surement pas compacte....
Par contre, une question un peu plus intéressante serait "est-ce que la réunion des est compacte" ? (là réponse est de nouveau "non", mais c'est un peu plus subtil)

P.S. : Met toi au MimeTeX ...

[kammi]

Salut,
Je comprend pas trop tes notation (principalement ton nk : c'est UNE variable que tu note nk ? c'est bizare comme truc...)

Ce que je crois comprendre de ton énoncé :

1) On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R (ou dans C ?) muni de la norme
.
2) Dans cet espace, on considère des parties de la forme :

où et
et ça donne l'impression que ce que toi tu considère, c'est les (ce qui personnellement me semble... pas très malin...)

Ta première question, ça semblait être "Est-ce que U(?,?) est compact" : là, c'est clair et on se fout des ? : c'est un fermé borné dans un e.v. de dim finie : c'est un compact.

La deuxième semble être "est-ce que la réunion des est compacte" et c'est là que le fait de prendre rend le truc "débile" : la réunion des n'est clairement pas bornée donc surement pas compacte....
Par contre, une question un peu plus intéressante serait "est-ce que la réunion des est compacte" ? (là réponse est de nouveau "non", mais c'est un peu plus subtil)

P.S. : Met toi au MimeTeX ...

non nk est un indice(c a d Unk est un ensemble dépend de nk)

[Ben314]

non nk est un indice(c a d Unk est un ensemble dépend de nk)

Bon, je comprend encore moins...
"nk est un indice" : un indice de QUOI ?
Si c'est un "n indice k", là, j'y comprend que dalle : vu que ton "n indice k" apparait systématiquement sous cette forme sans aucune référence à "k" tout seul, ça serait un chouilla plus malin de l'appeler n.
Moi, à ta place, je l'aurais appelé "n indice k indice j indice l" : ça aurait été plus clair...

Et ton fameux U, c'est donc bien (remarque bien que je met les indice k qui te tiennent tant à coeur...

Si c'est ça et que tu fait la réunion sur les "k" alors :
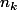
- Soit les sont bornés et la réunion est égale à celui correspondant au plus grand .
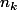
- Soit ils ne le sont pas et la réunion de est non bornée donc surement pas compacte.

Ou alors ton U, c'est pas une réunion (je te le redit : si tu veut te faire comprendre, fait l'effort de taper des trucs un peu propre en Mimetex...) et c'est uniquement UN ensemble du type U(?,?) et ça fait 10 fois qu'on te dit qu'il est trivial qu'un truc pareil est compact (fermé en dimension finie).

Ah, aussi,

est ce que U(nk) est compact dans ??

Un petit rappel de topologie : être compact, c'est une notion absolue et pas relative : ça ne sert absolument à rien de rajouter derrière "être compact dans quelquechose" (contrairement à "être fermé" par exemple).
Le seul truc qui peut être utile est de rajouter "compact pour..." au cas où tu ait plusieurs topologies sur le même espace (style topologie faible/forte), mais là, tu ne manipule que la topologie issue de la norme L².

[kammi]

Salut,
Je comprend pas trop tes notation (principalement ton nk : c'est UNE variable que tu note nk ? c'est bizare comme truc...)

Ce que je crois comprendre de ton énoncé :

1) On se place sur l'espace vectoriel E=L²([0,1]) des fonctions intégrables de [0,1] dans R (ou dans C ?) muni de la norme
.
2) Dans cet espace, on considère des parties de la forme :

où et
et ça donne l'impression que ce que toi tu considère, c'est les (ce qui personnellement me semble... pas très malin...)

Ta première question, ça semblait être "Est-ce que U(?,?) est compact" : là, c'est clair et on se fout des ? : c'est un fermé borné dans un e.v. de dim finie : c'est un compact.

La deuxième semble être "est-ce que la réunion des est compacte" et c'est là que le fait de prendre rend le truc "débile" : la réunion des n'est clairement pas bornée donc surement pas compacte....
Par contre, une question un peu plus intéressante serait "est-ce que la réunion des est compacte" ? (là réponse est de nouveau "non", mais c'est un peu plus subtil)

P.S. : Met toi au MimeTeX ...

merci beaucoup Ben314

en utilisant MimeTeXvoila mon ensemble U indice n indice k ""j'espere que ça sera clair comme""


avec c'est n indice k et c'est U indice

et ma question était ""pour un fixé cet ensemble est t il compact[B]??""[/B]

[Ben314]

Donc "ton" c'est effectivement "mon" et, comme tout les U(?,?), il est compact car c'est la boule fermée de rayon du s.e.v. de dim finie de L²([0,1]) engendré par les et pour .
(et Lionel t'avais donné la réponse 1/2h après la question...)

P.S. Entre la définition précédente et celle de ton 1er post, il y a un (1er post) qui est devenu un (post çi dessus), mais ça ne change rien à la compacité du bidule.

P.S.2 : J'avais pas vu la deuxième différence avec ton premier post : ça dessus, tu prend les et dans et ça fait que ton U, il est compact car il est... fini...

[kammi]

Donc "ton" c'est effectivement "mon" et, comme tout les U(?,?), il est compact car c'est la boule fermée de rayon du s.e.v. de dim finie de L²([0,1]) engendré par les et pour .
(et Lionel t'avais donné la réponse 1/2h après la question...)

P.S. Entre la définition précédente et celle de ton 1er post, il y a un (1er post) qui est devenu un (post çi dessus), mais ça ne change rien à la compacité du bidule.

P.S.2 : J'avais pas vu la deuxième différence avec ton premier post : ça dessus, tu prend les et dans et ça fait que ton U, il est compact car il est... fini...

je suis vraiment désolé pour ma mauvaise explication, ""dans mon ensemble les et sont dans c'est juste une faute de frappe""

[kammi]

une autre question s'il vous plait,

est ce que la réunion des sur tout les est dense dans ??

[Ben314]

Oui,
Il te suffit de considérer le polynôme trigo formé avec les coeff. de Fourrier d'indice

[kammi]

Oui,
Il te suffit de considérer le polynôme trigo formé avec les coeff. de Fourrier d'indice <n et d'utiliser l'égalité de Parseval pour conclure que le reste est aussi petit que tu veut.

pouvez vous m'expliquer un peu plus[SIZE=5]??[/SIZE]

[Ben314]

Si f est une fonction quelconque de L²([0,1]), on peut toujours calculer les coeff. de fourriers an et bn de f et l'égalité de Parceval te dit que la norme (dans L²) de f, vérifie .
Si pour tout n, on prend pour Pn le polynôme trigo. formé avec les ak et bk où alors Pn est évidement dans la réunion des Un et peut être rendu aussi petit qu'on veut à condition de prendre n suffisamment grand.

Ça montre que tu peut trouver des élément de la réunion des Un aussi proche que tu veut de n'importe quelle fonction f de L²([0,1]) CQFD

[kammi]

Si f est une fonction quelconque de L²([0,1]), on peut toujours calculer les coeff. de fourriers an et bn de f et l'égalité de Parceval te dit que la norme (dans L²) de f, vérifie .
Si pour tout n, on prend pour Pn le polynôme trigo. formé avec les ak et bk où alors Pn est évidement dans la réunion des Un et peut être rendu aussi petit qu'on veut à condition de prendre n suffisamment grand.

Ça montre que tu peut trouver des élément de la réunion des Un aussi proche que tu veut de n'importe quelle fonction f de L²([0,1]) CQFD

""on peut trouver des élément de la réunion des Un aussi proche qu'on veut de n'importe quelle fonction f de L²([0,1]) "" c'est ça la définition de la densité d'un ensemble dans L² ?

[Ben314]

""on peut trouver des élément de la réunion des Un aussi proche qu'on veut de n'importe quelle fonction f de L²([0,1]) "" c'est ça la définition de la densité d'un ensemble dans L² ?

Oui, et pas que dans L² d'ailleurs : c'est la définition d'une partie "dense" dans n'importe quel espace métrique...

[kammi]

Oui, et pas que dans L² d'ailleurs : c'est la définition d'une partie "dense" dans n'importe quel espace métrique...

je vous remerci infiniment.