je ne voie pas par ou commencé sauf essayer de faire des substitution ou un pivot de Gauss
Système
7 messages
- Page 1 sur 1
système
bonjours, je bloque sur la résolution d'un système:
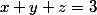


je ne voie pas par ou commencé sauf essayer de faire des substitution ou un pivot de Gauss
je ne voie pas par ou commencé sauf essayer de faire des substitution ou un pivot de Gauss
Salut,
Tu risque pas de faire "du pivot de Gauss" avec un système non linéaire !!!
Donc la seule méthode, c'est... les gros calculs ou... le flair...
Ici, avec un peu de flair, ça se fait assez bien (avec que des calculs bourrins style substitution, je sais pas trop...)
Tu risque pas de faire "du pivot de Gauss" avec un système non linéaire !!!
Donc la seule méthode, c'est... les gros calculs ou... le flair...
Ici, avec un peu de flair, ça se fait assez bien (avec que des calculs bourrins style substitution, je sais pas trop...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Tu risque pas de faire "du pivot de Gauss" avec un système non linéaire !!!
Donc la seule méthode, c'est... les gros calculs ou... le flair...
Ici, avec un peu de flair, ça se fait assez bien (avec que des calculs bourrins style substitution, je sais pas trop...)
j'ai envie d'utiliser le faite que
mais la je trouve une relation avec xy,xz,yz.( en remplacent le x+y+z et x²+y²+z²)
si je fait le même raisonnement avec la 3ème équation, j'aurais une autre relation similaire mais apres?
Après, lorsque tu as des équations "symétriques" comme là, le truc pas con, c'est d'utiliser ce qu'on appelle les "polynômes symétriques élémentaires".
Comme tu as pas du en entendre parler, ça consiste juste à constater que, si on développe le polynôme
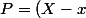(X-y)(X-z)) , on trouve
, on trouve 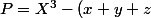X^2+(xy+yz+zx)X-xyz)
Donc si tu arrive à déduire de ton système les valeurs de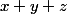 (ça c'est pas trop dur...) de
(ça c'est pas trop dur...) de  (c'est ce que tu as commencé à faire) et de
(c'est ce que tu as commencé à faire) et de 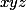 (là il faut utiliser la 3em équation et faire quelques calculs) alors, tu pourra écrire le polynôme P et vérifier... qu'il n'a pas 3 racines réelles (donc que le système n'a pas de solutions dans R)
(là il faut utiliser la 3em équation et faire quelques calculs) alors, tu pourra écrire le polynôme P et vérifier... qu'il n'a pas 3 racines réelles (donc que le système n'a pas de solutions dans R)
Comme tu as pas du en entendre parler, ça consiste juste à constater que, si on développe le polynôme
Donc si tu arrive à déduire de ton système les valeurs de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Après, lorsque tu as des équations "symétriques" comme là, le truc pas con, c'est d'utiliser ce qu'on appelle les "polynômes symétriques élémentaires".
Comme tu as pas du en entendre parler, ça consiste juste à constater que, si on développe le polynôme, on trouve
Donc si tu arrive à déduire de ton système les valeurs de(ça c'est pas trop dur...) de
(c'est ce que tu as commencé à faire) et de
(là il faut utiliser la 3em équation et faire quelques calculs) alors, tu pourra écrire le polynôme P et vérifier... qu'il n'a pas 3 racines réelles (donc que le système n'a pas de solutions dans R)
ah d'accord, donc les racines du polynôme me donnerons les valeurs de x,y et z.
pour trouvé xyz, je doit aussi partir de
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
