Limites, continuité

[OrsayMPI]

Bonjour,

Je galère un peu sur la correction d'un exo.

Enoncé : Soit f : R\{1/3} R telle que f(x) = (2x+3)/(3x-1).
Pour tout > 0, déterminer tel que :

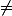
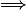
( x 1/3 et |x| ) | f(x) + 3 |

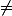
Correction : Soit > 0. Si x 1/3 , | f(x) + 3 | = | 11x / (3x - 1)|

On remarque que : | 3x - 1 | 1/2 ( x 1/2 ou x 1/6 )

Supposons que x 1/6 :

On a alors | f(x) + 3 | 22|x|

Si de plus |x| /22, alors | f(x) + 3 |

On a alors = min(1/6, /22 ).

Ce qui m'embête c'est la supposition x 1/6. Qu'est ce qui justifie cette supposition ? Comment sait - on que sera forcément inférieur à 1/6 ?

Merci d'avance

[Doraki]

Tu le sais parceque c'est TOI qui vas le choisir, le delta.
Dans ce genre de problème, il faut bien comprendre que si un delta > 0 marche, alors n'importe quel delta' entre 0 et delta va encore marcher.
Plus delta est petit et plus il fait marcher la condition qu'il est censé vérifier.

Du coup tu ne risques JAMAIS de te bloquer en décidant arbitrairement de prendre delta' plus petit qu'un réel > 0 fixe.

[Sylviel]

on te demande de trouver un delta tel que ...
tu peux donc le choisir aussi petit que tu le souhaites. Si ça t'arrange qu'il soit plus petit que 1/6 alors vas-y !

[deltab]

Bonjour.

@OrsayMPI.

L'exercice proposé revient à montrer en utilisant la définition de la limite que .

On a .
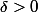
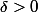
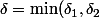Il est clair que l'on choisit un tel que , alors n'est pas bornée, il faut donc éviter ça et prendre un tel que donc éviter que 3x-1=0, il suffit de choisir tel que ce qu'on a fait en prenant ce qui a donné x1/2. Ceci va donner . Si , alors . Il ne faut oublier que donc prendre . Les deux conditions et seront vérifiées si l'on prend c'est ce qu'a fait en prenant . Reste à vérifier que