bonjours, j'ai une question sur un exercice de base sur les polynôme:
je doit déterminer tous les polynôme de de R[X] tel que P=P'P''
j'ai trouver que le degré de P doit être de 3 en disant que deg(P)=deg(P')+def(P")
et en appelant n le degré de P. est ce que cette argument est correct.
pour trouver P, j'ai penser à prendre différente valeur de x pour trouver les coefficients du polynôme mais ça ne va me donner quune solution?
Polynome, recherche
8 messages
- Page 1 sur 1
naru2 a écrit:bonjours, j'ai une question sur un exercice de base sur les polynôme:
je doit déterminer tous les polynôme de de R[X] tel que P=P'P''
j'ai trouver que le degré de P doit être de 3 en disant que deg(P)=deg(P')+def(P")
et en appelant n le degré de P. est ce que cette argument est correct.
pour trouver P, j'ai penser à prendre différente valeur de x pour trouver les coefficients du polynôme mais ça ne va me donner quune solution?
Salut
Pose
calcule
Attention aux cas particuliers.
Il y a une infinité de solutions.
Salut,
1) Attention a commencer par étudier le(s) cas où le degré n'existe pas (i.e. où l'un des polynôme est nul) AVANT d'écrire l'équation concernant les degré.
2) Si ça t'amuse, une solution alternative au fait de dériver le polynôme puis d'identifier les coeff. ça peut être de dire que=a+bX+cX^2+dX^3) signifie très exactement que
signifie très exactement que 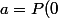,\ b=P'(0),\ c=\frac{P''(0)}{2!}\ d=\frac{P'''(0)}{3!}) donc chercher
donc chercher 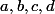 équivaut à chercher les dérivées successives en 0.
équivaut à chercher les dérivées successives en 0.
Or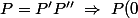=P'(0)P''(0)\ \Rightarrow\ a=2bc) ,
,
En dérivant,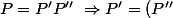^2+P'P'''\ \Rightarrow\ b=(2c)^2+6bd) ,
,
etc.
Évidement (et heureusement...) on tomber sur les mêmes équations que celles qu'on obtiendrait et dérivant puis en identifiant les coefficients...
3) Si tu veut encore plus t'amuser, tu peut aussi raisonner sur les racines (éventuellement complexes) des polynômes :
Vu que P=P'P", toute racine de P' est elle même racine de P donc si elle est racine d'ordre d de P', elle est racine d'ordre d+1 de P.
Si les racines de P' sont a1,a2,...ak d'ordres respectifs d1,d2,...dk donc avec d°(P')=d1+d2+...dk, alors ces mêmes a1,a2,...ak sont racines de P d'ordre d1+1,d2+1,...,dk+1 donc d°(P)=(d1+1)+(d2+1)+...+(dk+1). Sauf que d°(P)=d°(P')+1 donc on a forcément k=1 ce qui signifie que P admet une unique racine.
P est donc forcément de la forme=\lambda(X-\alpha)^d) et en injectant ça dans
et en injectant ça dans  on trouve immédiatement que
on trouve immédiatement que 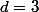 puis que
puis que 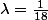 .
.
Par contre est quelconque ce qui n'est pas étonnant vu que la formule
est quelconque ce qui n'est pas étonnant vu que la formule  est "stable par translation", c'est à dire que, si P(X) vérifie la formule alors P(X+a) aussi.
est "stable par translation", c'est à dire que, si P(X) vérifie la formule alors P(X+a) aussi.
1) Attention a commencer par étudier le(s) cas où le degré n'existe pas (i.e. où l'un des polynôme est nul) AVANT d'écrire l'équation concernant les degré.
2) Si ça t'amuse, une solution alternative au fait de dériver le polynôme puis d'identifier les coeff. ça peut être de dire que
Or
En dérivant,
etc.
Évidement (et heureusement...) on tomber sur les mêmes équations que celles qu'on obtiendrait et dérivant puis en identifiant les coefficients...
3) Si tu veut encore plus t'amuser, tu peut aussi raisonner sur les racines (éventuellement complexes) des polynômes :
Vu que P=P'P", toute racine de P' est elle même racine de P donc si elle est racine d'ordre d de P', elle est racine d'ordre d+1 de P.
Si les racines de P' sont a1,a2,...ak d'ordres respectifs d1,d2,...dk donc avec d°(P')=d1+d2+...dk, alors ces mêmes a1,a2,...ak sont racines de P d'ordre d1+1,d2+1,...,dk+1 donc d°(P)=(d1+1)+(d2+1)+...+(dk+1). Sauf que d°(P)=d°(P')+1 donc on a forcément k=1 ce qui signifie que P admet une unique racine.
P est donc forcément de la forme
Par contre
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
bonjours, et merci de vos réponses,
donc je doit faire les cas ou P=0, P'=0 et P"=0
daccord je vais essayer les deux méthodes,
je voulais savoir, si j'ai une relation avec les dérivées,une des méthodes pour trouver les coefficients est d'utiliser la formule de Taylor?
que veut dire la notation d° ?
donc je doit faire les cas ou P=0, P'=0 et P"=0
daccord je vais essayer les deux méthodes,
je voulais savoir, si j'ai une relation avec les dérivées,une des méthodes pour trouver les coefficients est d'utiliser la formule de Taylor?
que veut dire la notation d° ?
naru2 a écrit:d'accord, mais juste je ne voit pas doù sort le k=1 quand j'écrit d1+d2+..dk=d1+1+d2+1+...dk+1+1?
Le "+1" en plus, il est de l'autre coté du égal.
Et, vu que 1+1+1+...+1 (k fois), ça fait k, lorsque tu retranche d1+d2+...+dk des deux cotés, il reste k=1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
